2020-07-12
322
Пусть 
непрерывна на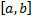 
, 
– ее первообразная. Тогда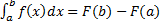 
.
Док-во: пусть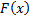 
– произвольная первообразная. Рассмотрим 
– также первообразная. Тогда 
. Возьмем 
. Т.к. 
, то 
, т.е. 
. При 
: 
или 
:
Пример.
.
Вычисление определенного интеграла подстановкой и по частям. Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат, интегрирование периодических функций.
Пусть непрерывна на 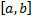, функция 
имеет непрерывную производную на 
, причем 
. Тогда 
.
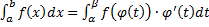Док-во: пусть 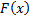–первообразная для на 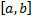, т.е. 
. Тогда по формуле Ньютона-Лейбница: . Функция 
– первообразная для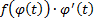 
, по формуле Ньютона-Лейбница: 
Пример.
Интегрирование по частям в определенном интеграле.
Пусть функции 
и 
имеют непрерывные производные на [ 
.
Тогда 
, т.е. 
Док-во: 
, т.е. 
Пример.
Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат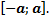 
Рис. 6
Теорема. Пусть интегрируема на 
, тогда:
1. Если – четная, то 
.
2. Если – нечетная, то 
.
Док-во: 
(по свойству аддитивности) (см. рис. 6).
– для четной функции,
– для нечетной функции.
Пример.
Интегрирование периодических функций.
| Рис. 7 |
Пусть – периодическая с периодом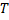 
, (т.е. 
), интегрируемая на 
Тогда 
и
(см. рис. 7).
Несобственные интегралы 1-го и 2-го рода, их свойства. Признаки сходимости. Абсолютная и условная сходимость несобственных интегралов.
Несобственные интегралы 1-го рода
Пусть определена на 
и интегрируема на любом отрезке вида 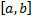. Зафиксируем 
и рассмотрим определенный интеграл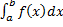 
.
Опр. Несобственным интегралом 1 рода функции от 
до 
называется предел при 
определенного интеграла от до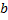 
:
| Рис. 8 |
Если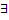 
конечный предел 
, то несобственный интеграл от до называется сходящимся, в противном случае (т.е. если предел равен 
или не существует) – расходящимся.
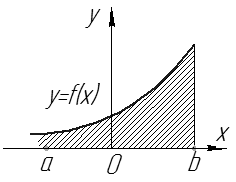
Геометрический смысл – площадь бесконечной фигуры, ограниченной линиями 
(см. рис. 8).
| Рис. 9 |
, определенной на 
по определению
(см. рис. 9).
Свойство линейности.
Если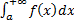 
, 
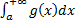сходятся, то сходятся интегралы
.
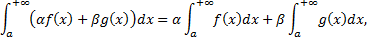
Аналогично для .
