Определенный интеграл как предел интегральных сумм

Пусть функция  определена на .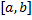

Опр. Разбиением 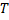 отрезка  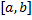называется совокупность точек 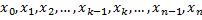, где .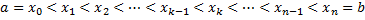

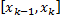 – элементарный отрезок (),

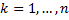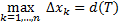,  – диаметр разбиения .

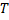Выберем произвольные точки

Рис. 1

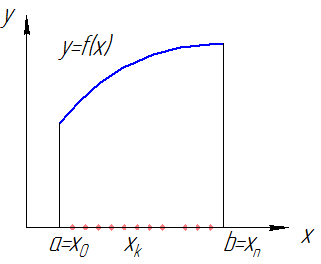Опр. Интегральной суммой функции , соответствующей разбиению 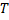 отрезка  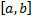и выбору точек  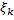(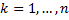) называется величина 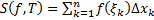(см. рис. 1).

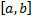Опр. Определенным интегралом функции  на отрезке  называется конечный предел при  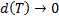интегральных сумм 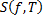, если он существует и не зависит от способа разбиения отрезка и выбора точек .

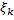Обозн.: 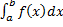, т.е.

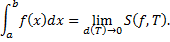
Тогда масса неоднородного стержня: ; координата точки: .

Опр. Если для функции  существует 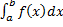, то функция называется интегрируемой (по Риману) на .

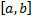Теорема (необходимое условие интегрируемости.)

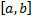Пусть функция  интегрируема на , тогда  ограничена на .

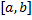Теорема (достаточное условие интегрируемости 1).

Непрерывная на 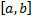 функция  является интегрируемой на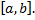

Теорема (достаточное условие интегрируемости 2).

Пусть 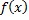 непрерывна на  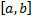кроме конечного числа точек разрыва первого рода , тогда  является интегрируемой на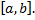

Геометрическая интерпретация определенного интеграла. , непрерывна на

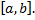
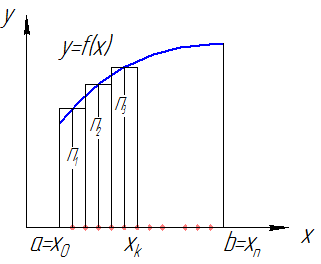
Рис. 2

.

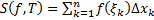 – площадь прямоугольника 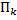 со сторонами 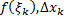(см. рис. 2).

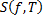 – площадь ступенчатой фигуры

При 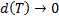 получим площадь криволинейной трапеции, ограниченной графиком функции  сверху, осью  снизу и прямыми .