Тема: «Производная степенной функции»
Производной функции 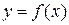 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 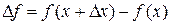 к приращению независимой переменной
к приращению независимой переменной 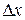 при стремлении последнего к нулю:
при стремлении последнего к нулю:
 (1)
(1)
Обозначения производной в точке х 0:
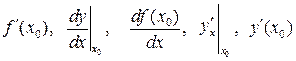 и другие.
и другие.
Если функция в точке х 0 (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).
Процесс отыскания производной называется дифференцированием.
Пример: Найти производную функции, используя ее определение 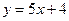
Решение:
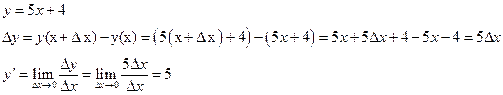
Основные формулы: 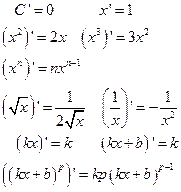
Пример: Вычислить производные функций:
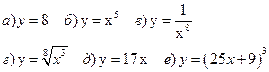
Решение:

Формулы дифференцирования основных элементарных функций

Пример. Найти производные функций:
а) 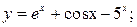
Решение.
а) Используя правила и формулы, получим:
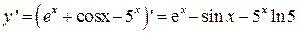
Самостоятельная работа
1.Найти производные функций
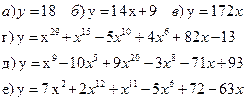
2.Найти производные функций
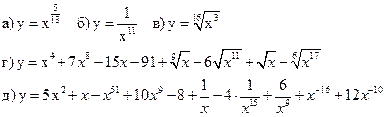
3) 
«Правила дифференцирования: производные произведения и частного»
Производной функции 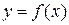 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 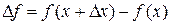 к приращению независимой переменной
к приращению независимой переменной 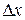 при стремлении последнего к нулю:
при стремлении последнего к нулю:
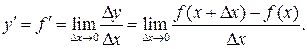
Правила дифференцирования
| № пп | U = u (x), V = V (x) - дифференцируемые функции |
| I | 
|
| II | 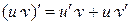
|
| III | 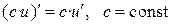
|
| IV | 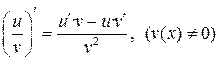
|
| V | 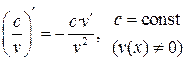
|
Пример. Найти производные функций:
а) 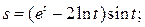 б)
б) 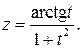
Решение.
а) Используя правила дифференцирования произведения функций, разности, формулы и учитывая, что независимая переменная есть t, т. е. t =1, получим:

б) Используя правила дифференцирования частного, суммы
и формулы, учитывая, что t =1, получим:
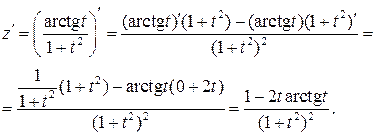
Самостоятельная работа
Найти производные функций:
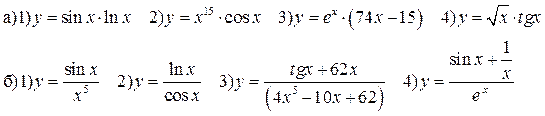
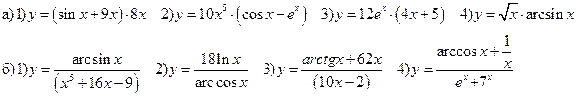
Тема: «Производная сложной функции»
Производной функции 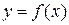 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 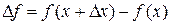 к приращению независимой переменной
к приращению независимой переменной 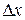 при стремлении последнего к нулю:
при стремлении последнего к нулю:
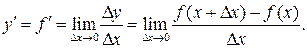
Производная сложной функции 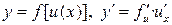 .
.
Производной n-го порядка называется производная от производной (n –1)-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции.
Производная второго порядка 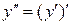 или
или 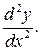
Производная третьего порядка 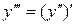 или
или 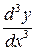 и т. д.
и т. д.
Пример. Найти производную функции 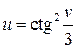
Решение: Сложная степенная функция, независимая переменная есть v,
т. е. v =1; используя формулу, получим:
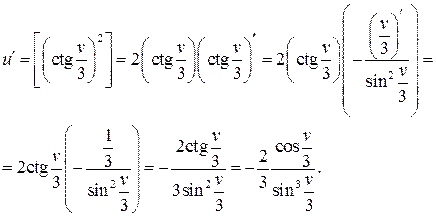
 2020-07-12
2020-07-12 65
65







