Если 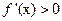 на промежутке, то функция
на промежутке, то функция 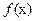 возрастает на этом промежутке. Если
возрастает на этом промежутке. Если 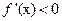 на промежутке, то функция
на промежутке, то функция 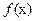 убывает на этом промежутке.
убывает на этом промежутке.
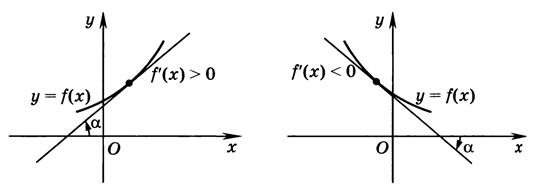
Промежутки возрастания и убывания функции называют промежутками монотонности функции.
Пример: Найти интервалы возрастания и убывания функции 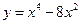
Решение: Найдем
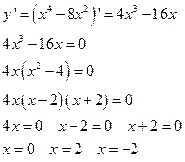
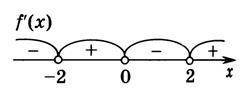
С помощью метода интервалов находим интервалы возрастания и убывания функции.
Функция возрастает при 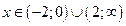 , убывает при
, убывает при 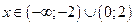
Точки, в которых производная равна нулю, называются стационарными точками. Точки, в которых функция либо недифференцируема (не имеет производной), либо имеет производную, равную нулю, называются критическими точками этой функции.
Точка х0 называется точкой максимума функции 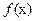 , если существует такая окрестность точки х0, что для всех
, если существует такая окрестность точки х0, что для всех 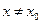 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 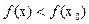 .
.
Точка х0 называется точкой минимума функции 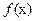 , если существует такая окрестность точки х0, что для всех
, если существует такая окрестность точки х0, что для всех 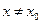 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 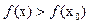 .
.
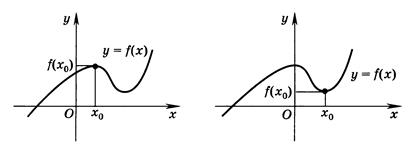
Точки максимума и минимума называются точками экстремума.
Пример: Найти стационарные точки функции 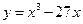
Решение:
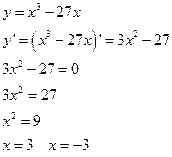
Пример: Найти точки экстремума функции 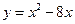
Решение:
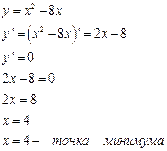
Пример: Найти значение функции в точках экстремума 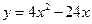
Решение:
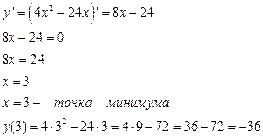
Самостоятельная работа
1) Найти промежутки возрастания и убывания функции
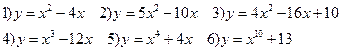
2) Найти стационарные точки функции
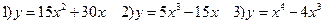
3) Найти точки экстремума функции и значения функции в этих точках
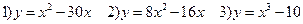
 2020-07-12
2020-07-12 68
68








