Самостоятельная работа

1) Найти производные функций:

2) Найти производные второго порядка:

3) Найти производные третьего порядка:

 

Тема: «Уравнения касательной и нормали»

Геометрический смысл производной.

Если кривая задана уравнением ,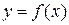
то — угловой коэффициент касательной к графику функции в этой точке ().

Уравнение касательной к кривой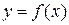  
в точке х₀ (прямая М₀Т) имеет вид:

                                                                 

а уравнение нормали (М₀N):

                                       

Пример. Составить уравнение касательной и нормали к кривой в точке с абсциссой х ₀=-2.

Используем уравнения касательной (2) и нормали (3):

1)

2)

Подставим  в уравнения и получим:

или  — уравнение касательной.

 или — уравнение нормали.

                   

Самостоятельная работа

1.Составить уравнение касательной к графику функции в точке с абсциссой х₀

2.Составить уравнение нормали к графику функции в точке с абсциссой х₀