2020-07-12
112
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между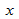 
и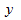 
нет линейного соотношения: изменение 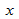не влияет на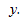 
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент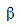 
равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению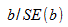 
, которая подчиняется 
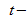распределению с 
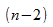степенями свободы, где 
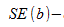стандартная ошибка коэффициента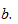 
, 
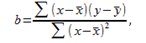
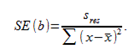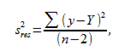- оценка дисперсии остатков.
Обычно если достигнутый уровень значимости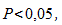 
нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :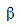 
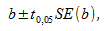
где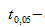 
процентная точка 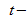распределения со степенями свободы 
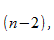что дает вероятность двустороннего критерия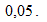 
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем,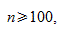 
мы можем аппроксимировать 
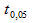значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
