2020-08-05
149
Идея линеаризации заключается в том, что в системах регулирования (поддержания заданных значений величин) сигналы мало отклоняются от рабочей точки - некоторого положения равновесия, в котором все сигналы имеют «правильные» значения и их производные равны нулю. Поэтому для решения задач управления часто достаточно использовать линейную модель в отклонениях от этой рабочей точки.
Пример бак с водой. В нижней части бака просверлено отверстие, через которое вытекает вода: 
- площадь сечения бака по всей его высоте, 
- площадь сечения отверстия, 
- расход вытекающей воды, 
-уровень воды в баке определяется как интеграл от потока воды , деленный на : 
.
СЛАЙД 7. Связь уровня воды () с расходом можно найти с помощью закона Бернулли, который в данном случае принимает вид 
, где 
- плотность жидкости, g=9,81 м/с2 - ускорение свободного падения, 
- скорость вытекания жидкости. Отсюда получаем 
. Учитывая, что расход воды вычисляется как 
, находим (1)
, (1)
где 
- постоянная величина. Это статическая модель, потому что она не содержит производных, характеризующих изменение сигналов во времени. Статическая модель описывает установившееся состояние (статический режим), когда в баке поддерживается постоянный уровень воды и поток вытекающей воды тоже постоянный.
Очевидно, что модель (1) - нелинейная, поскольку содержит 
Линеаризовать ее - значит приближенно заменить уравнение (1) линейным уравнением 
, где 
- некоторый коэффициент. Тогда один из вариантов - вычислить коэффициент как угол наклона отрезка в интервале от 0 до 1 м, соединяющего точки кривой на концах этого интервала. Для определенности далее везде принимаем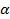 
=1, тогда получаем =1. 
СЛАЙД 8. Конечно, эта модель очень грубая и дает большую ошибку, особенно для уровней в диапазоне от 0,1 до 0,6. Чтобы уменьшить ошибку, можно попробовать несколько изменить (например, увеличив его до 1,2), однако точность приближения по-прежнему будет невысокая, хотя лучше, чем в первом случае, если обычно уровень мало изменяется вблизи среднего значения =0,5 м можно применить другой подход. В этой области кривая (1)почти совпадает с касательной в точке (0,5; 
) угол наклона которой равен производной (2)
. (2)
Уравнение касательной, проходящей через точку (0,5; ), имеет вид (3):
. (3)
Свободный член определим 
по равенству (4):
(4)
Так получаем модель (5)
(5)
Это линейное уравнение, однако модель (2) – нелинейная, поскольку для нее не выполняется, например, свойство умножения на константу. Это легко проверить, сравнив 
и 
: 
, 2⋅ 
.
Принцип суперпозиции также не выполняется
Для того, чтобы получить из (5) линейную модель, нужно записать уравнения в отклонениях от рабочей точки (
), в которой мы определили наклон касательной. Из (5) следует, что (6)
(6)
Поскольку график зависимости (5) проходит через точку (), можно применить равенство (7)
. (7)
СЛАЙД 9. Тогда из (6) находим (8)
(8)
Полученное таким образом уравнение - это линейная модель объекта, записанная в отклонениях входа и выхода от номинальной (рабочей) точки (). Приближенная модель (6) точнее всего соответствует объекту вблизи этой точки, а при больших отклонениях от нее ошибка может значительно возрастать.
