Импульсная характеристика (весовая функция)

       СЛАЙД 17. В принципе, в качестве тестового сигнала можно использовать любой сигнал. Например, прямоугольный импульс. На рисунках а)-в) показаны три импульса, имеющих одинаковые площади. Для простоты изложения будем считать, что эта площадь равна единице.

Если уменьшать ширину импульса, сохраняя его площадь, высота импульса будет расти и в пределе (когда ширина стремится к нулю) станет бесконечной. Такой сигнал называется импульсом или дельта-функцией Дирака . Это классический тестовый – идеальный, невозможный в реальной жизни сигнал, который равен нулю во всех точках, кроме , где он уходит в бесконечность, причем его площадь (интеграл по всей оси времени) равна единице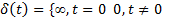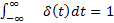: (5)

, .                                (5)

Поскольку бесконечный импульс невозможно нарисовать, на графике он изображается стрелкой, высота которой равна единице (см. рисунок г).

Иногда определяют дельта-функцию как производную от единичного ступенчатого сигнала 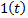 . Действительно, эта производная равна нулю при всех значениях t, кроме нуля, где она обращается в бесконечность.

Реакция системы на единичный импульс (дельта-функцию) называется импульсной характеристикой и обозначается  как на рисунке:

Импульсная характеристика, так же, как и переходная характеристика, определяется при нулевых начальных условиях, то есть, объект должен находиться в состоянии покоя.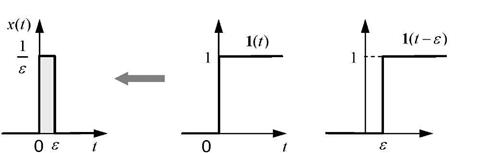

Рассматривая, дельта-функцию как предельный случай прямоугольного сигнала единичной площади, можно найти связь между переходной функцией и импульсной характеристикой. Если ширина прямоугольного импульса равна , а высота -  импульс можно представить в виде разности двух ступенчатых сигналов 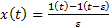(6):

,                                                    (6)

 где 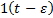 - это единичный ступенчатый сигнал, который приходит в момент , то есть, смещен по времени на  (см. рисунок далее).

       Так как для линейных систем справедлив принцип суперпозиции, сигнал на выходе будет равен разности реакций системы на входы 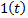 и 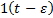, умноженной на коэффициент . Учитывая, что реакция на сигнал 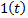 - это переходная функция , получаем 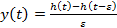(7)

                                                  (7)

       Переходя к пределу по , находим что импульсная характеристика (8):

                        (8)

как оказывается, равна производной от переходной функции. Наоборот, переходная функция — это интеграл от импульсной характеристики на интервале от 0 до t 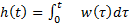(9):

.                                              (9)

       Дифференцируя переходную характеристику (8) звена первого порядка, получаем соответствующую импульсную характеристику 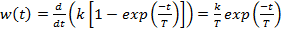(10):

                                 (10)

Другое название импульсной характеристики - весовая функция.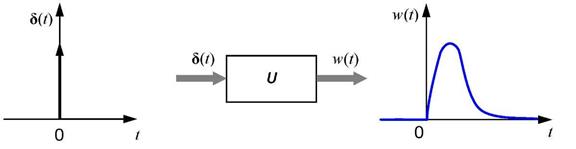

СЛАЙД 19. Это название связано с тем, что для произвольного входного сигнала 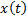 выход системы  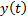при нулевых начальных условиях вычисляется как интеграл 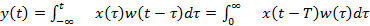(11)

                                   (11)

В отличие от ступенчатого сигнала, мгновенный импульс бесконечной величины невозможно получить на реальном устройстве, поэтому снять импульсную характеристику системы, строго говоря, экспериментально не удается.