1.1.Матрицы и определители.
Матрицы. Пусть m и n – натуральные числа.
Матрицей размера m 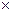 n называется прямоугольная таблица чисел
n называется прямоугольная таблица чисел 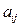 из m строк и n столбцов:
из m строк и n столбцов:
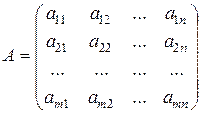 , i = 1…m, j = 1,…,n.
, i = 1…m, j = 1,…,n.
Здесь m – число строк в матрице А; i – номер строки (1 ≤ i ≤ m); n – число столбцов; j – номер столбца (1 ≤ j ≤ n); аij – элемент матрицы А, находящийся в i –й строке и j –м столбце. Матрицу А удобно обозначать (аij)mn. По матрице А можно построить транспонированную матрицу А т, сделав строки матрицы А столбцами с теми же номерами.
Две матрицы А = (аij)mn и В = (bij)pq называются равными, если m = p,
n = q, aij = bij для всех значений i,j.
Матрица размера 1 × n называется матрицей-строкой, матрица размера m×1 называется матрицей-столбцом.Матрица А =  называется квадратной порядка n, если число строк равно числу столбцов (m = n). Квадратная матрица Е порядка n называется единичной, если у неё на главной диагонали стоят единицы, а на всех остальных местах – нули:
называется квадратной порядка n, если число строк равно числу столбцов (m = n). Квадратная матрица Е порядка n называется единичной, если у неё на главной диагонали стоят единицы, а на всех остальных местах – нули:
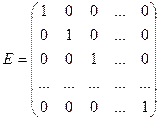 .
.
Матрица Аt, полученная из данной матрицы А заменой каждой ее строки столбцом с тем же номером, называется транспонированной относительно А.
Сложение матриц и умножение их на число. Пусть А = (аij) и
В = (bij) матрицы размера m×n.
Суммой матриц А и В называется матрица С, для которой
cij = aij + bij, (1)
где 1 ≤ i ≤ m, 1 ≤ j ≤ n (то есть, чтобы сложить две матрицы, нужно сложить их соответствующие элементы).
Произведением матрицы А на число называется матрица А =
= (аij)mn (то есть, чтобы умножить матрицу на число, нужно каждый элемент этой матрицы умножить на это число).
Пример 1. Пусть А =  В =
В = 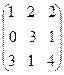 .
.
Вычислить матрицу 4А + 5В - 2В Т.
Решение. Чтобы умножить матрицу на число, нужно каждый элемент этой матрицы умножить на это число. Чтобы сложить матрицы одинаковых размеров, нужно сложить одноименные элементы этих матриц, В t = 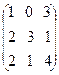 - матрица, транспортированная к матрице В. Тогда
- матрица, транспортированная к матрице В. Тогда
4А + 5В – 2 В t = 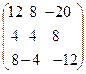 +
+ 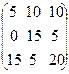 +
+ 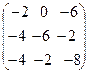 =
= 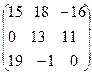 .
.
Произведение матриц. Пусть А =  и В =
и В = 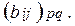 Произведение матриц существует, если число столбцов первой матрицы равно числу строк второй матрицы. Перемножаются матрицы А и В по правилу: i-я строка первой матрицы А умножается скалярно на j - й столбец матрицы В, и полученное число Сij записывается в j - й столбец на i - е место искомой матрицы С:
Произведение матриц существует, если число столбцов первой матрицы равно числу строк второй матрицы. Перемножаются матрицы А и В по правилу: i-я строка первой матрицы А умножается скалярно на j - й столбец матрицы В, и полученное число Сij записывается в j - й столбец на i - е место искомой матрицы С:
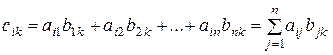 . (2)
. (2)
Свойства произведения матриц:
1. 
2. 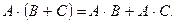
Произведение матриц, вообще говоря, не коммутирует, т. е. 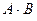 не всегда равно
не всегда равно  .
.
Пример 2. Даны две матрицы:
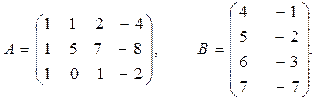
Найти произведение АВ. Можно ли получить произведение ВА?
Решение. Число столбцов матрицы А равно числу строк матрицы В, поэтому произведение АВ определено. Умножая строку матрицы А на столбец матрицы В, по формуле (2) получаем
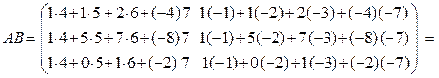
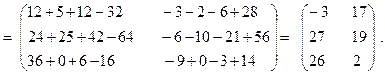
Произведение ВА не определено, так как число столбцов матрицы В не равно числу строк матрицы А.
Целой положительной степенью АК (к > 1) квадратной матрицы А называется произведение к матриц, каждая из которых равна А.
Многочленом степени к (к – целое неотрицательное число) от квадратной матрицы А называется выражение вида

Пример 3. Найти P(A), если P(x) = x2 – 3x + 5 и  .
.
Решение. В соответствии с определением многочлена от матрицы  получаем P(A) = A2 –3A + +5E или
получаем P(A) = A2 –3A + +5E или

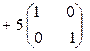
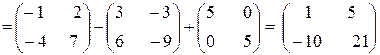 .
.
Определители. Определителем квадратной матрицы 2-го порядка называется число
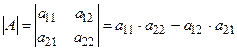 .
.
Определителем квадратной матрицы 3-го порядка называется число

Минором какого-либо элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, которым принадлежит данный элемент. Алгебраическим дополнением элемента аik определителя называется его минор, взятый со знаком (-1)i + k.
Свойства определителей:
- если поменять местами две соседние строки определителя, то он изменит знак;
- если две строки равны, то он равен нулю;
- если поменять местами строку и соответствующий столбец, то определитель не изменится;
- если все элементы некоторой строки умножить на одно и то же число, то определитель умножится на это число;
- если соответствующие элементы двух строк определителя пропорциональны, то он равен нулю;
- если каждый элемент некоторой строки определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки, кроме указанной, прежние, а в данной строке в первом определителе стоят первые, а во втором вторые слагаемые;
- при прибавлении к элементам любой строки соответствующих элементов какой-либо другой строки, умноженных на одно и то же число, величина определителя не изменится;
- определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения.
Данные свойства можно сформулировать и для столбцов матрицы.
Пример 4. Вычислить определитель третьего порядка тремя способами: 1) по определению; 2) разложить по элементам 1-й строки;
3) преобразованием его с помощью свойств определителя:
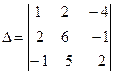
Решение:
1. D = 1×6×2 + 2(-1)(-1) + 2×5(-4) – (-4)6×(-1) –2×2×2 -1×5(-1) = -53.
2. Раскладываем по элементам 1-й строки 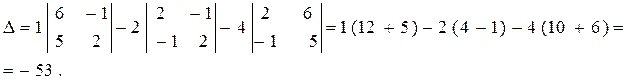 3. Умножая первую строку на (-2) и прибавляя ко второй, затем первую строку прибавляем к третьей, получаем
3. Умножая первую строку на (-2) и прибавляя ко второй, затем первую строку прибавляем к третьей, получаем
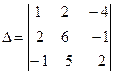
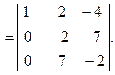
Разлагая этот определитель по элементам первого столбца, находим

Обратная матрица. Матрицей, обратной квадратной матрице А, называется квадратная матрица А-1, удовлетворяющая равенствам
АА-1 = А-1А = Е,
где Е – единичная матрица.
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. Всякая невырожденная квадратная матрица имеет единственную обратную матрицу

где Аij – алгебраическое дополнение элемента аij матрицы А.
1.2.Системы линейных уравнений
Пусть дана система m линейных уравнений с n неизвестными:
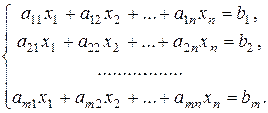 (4)
(4)
Эту систему можно записать в матричной форме: AX = B,
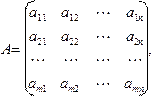 |  |
где
Решением системы называется всякая матрица-столбец X, обращающее матричное уравнение AX = B в тождество. Система называется совместной, если она имеет решение, и несовместной, если решений нет. Совместная система называется определенной, если решение единственное, и неопределенной, если она имеет бесконечно много решений. Система называется однородной, если ее свободные коэффициенты равны нулю.
Всякая квадратичная невырожденная матрица имеет единственную обратную матрицу. Найдя произведение А∙Х, замечаем, что систему уравнений (3) можно записать в виде А∙Х = В. Чтобы решить систему А∙Х = В матричным методом, умножим обе части этого равенства слева на А-1 и получим А-1 ∙ А∙Х = А-1 ∙ В, но А-1 ∙ А = Е, Е∙Х =Х, значит
Х = А- 1 ∙ В.
Правило Крамера. Если m = n и Δ = det A ≠ 0, то решение системы можно получить по формулам Крамера:
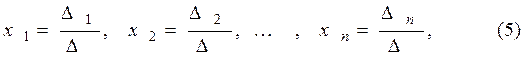
где Δ i (i = 1,2,…,n) – определитель, получаемый из определителя Δ заменой i‑го столбца на столбец свободных членов.
Две системы называются равносильными, если каждое решение одной является решением другой, т.е. у них множества решений совпадают. Следующие элементарные преобразования переводят систему в равносильную:
а) перемена местами любых двух уравнений;
б) умножение обеих частей любого уравнения на неравное нулю число;
в) прибавление к обеим частям любого уравнения соответствующих частей другого уравнения, умноженных на произвольное число.
Данные преобразования проще выполнять над матрицей, составленной из коэффициентов при неизвестных переменных и свободных членов. Такая матрица называется расширенной матрицей системы:

(6)
Метод Гаусса. Метод последовательного исключения неизвестных, или метод Гаусса, применим к любой системе линейных уравнений. Решая систему этим методом, преобразования совершаются не над уравнениями, а над расширенной матрицей. Это метод приведения расширенной матрицы системы к треугольному виду. Рассмотрим данный метод на примере.
Пример 7. Решить систему: а) средствами матричного исчисления; б) методом Гаусса; в) с помощью формул Крамера.
 4x - 3y +2z = 9;
4x - 3y +2z = 9;
2x +5y - 3z = 4;
5x +6y - 2z = 18.
Решение:
1. Вычислим определитель системы: 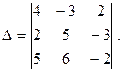
Разложим по элементам 1-й строки:
 так как
так как 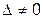 , то система имеет единственное решение.
, то система имеет единственное решение.
Пусть А-матрица коэффициентов при неизвестных, Х-матрица – столбец неизвестных и В-матрица – столбец из свободных членов:
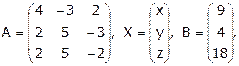 тогда
тогда 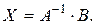
Для нахождения обратной матрицы 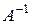 вычислим алгебраические дополнения элементов матрицы А:
вычислим алгебраические дополнения элементов матрицы А:
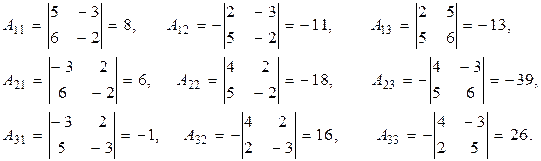
Обратная матрица определяется формулой (3)

Тогда
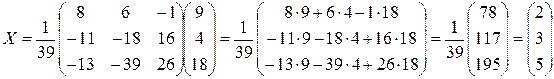
Итак, x = 2, y = 3, z = 5.
2. Составляем расширенную матрицу системы:
 Умножим 1-ую строку на
Умножим 1-ую строку на  и
и 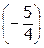 и прибавим соответственно ко второй и третьей строке:
и прибавим соответственно ко второй и третьей строке:
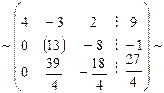 Умножим теперь вторую строку на
Умножим теперь вторую строку на 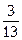 и
и 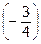 и прибавим соответственно к 1-й и третьей строке:
и прибавим соответственно к 1-й и третьей строке:
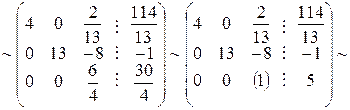 Умножим третью строку на
Умножим третью строку на 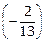 и 8, прибавим соответственно к 1-й и 2-й:
и 8, прибавим соответственно к 1-й и 2-й:
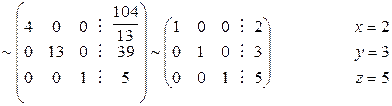
3. Если 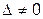 , то система
, то система 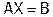 имеет единственное решение, которое можно найти по формуле (5).
имеет единственное решение, которое можно найти по формуле (5).
Итак, 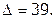

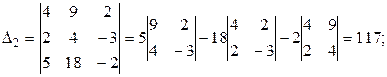
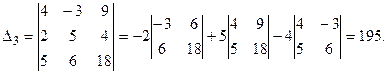
Тогда 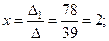
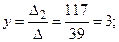
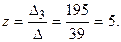
Ответ: х = 2, у = 3, z = 5.
 2020-08-05
2020-08-05 113
113







