2020-08-05
139
№1. Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.
Решение:
Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:
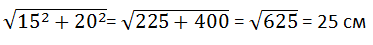
А теперь найдём объём параллелепипеда:
V = 15 ∙ 20 ∙ 25 = 7500 см3
Ответ: V = 7500 см3.
№2. Найти объем прямой треугольной призмы высотой 6, в основании которой - прямоугольный треугольник с катетами 3 и 7.
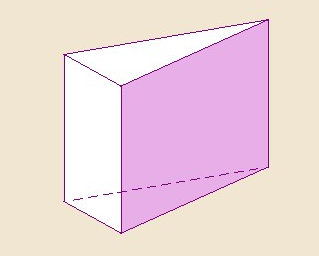
Решение: Объем призмы вычисляется по формуле
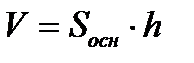, т.к. в основании призмы – прямоугольный треугольник, то объем призмы будет вычисляться по формуле
,
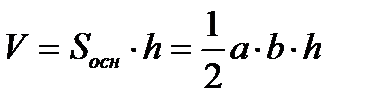где а и в – катеты треугольника. Подставляя все данные задачи в формулу, получаем ответ:
.
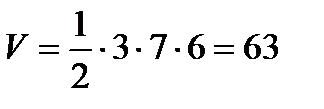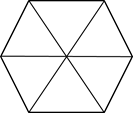
№3. Найти объём правильной -угольной призмы, у которой каждое ребро равно а, если: а) n=3, б) n=4, в) n=6.
Решение: поскольку призма правильная, значит, это прямая призма и в основании лежит правильный многоугольник.
Формулу для вычисления объёма прямой призмы мы только что вывели 
. Поскольку, по условию все ребра призмы равны a, значит, высота призмы равна h=a. Осталось найти площадь основания.
Основанием правильной треугольной призмы является правильный, то есть равносторонний треугольник n=3. Площадь правильного треугольника со стороной f вычислить несложно, она равна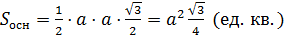 
.
Применяя формулу для вычисления объёма прямой призмы, получим, что объём правильной треугольной призмы равен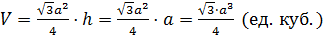 
.
Основанием правильной четырёхугольной призмы является квадрат n=4. Площадь квадрата со стороной a равна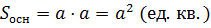 
. Тогда объём правильной четырёхугольной призмы равен 
.
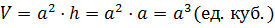Основанием правильной шестиугольной призмы является правильный шестиугольник n=6. Своими большими диагоналями шестиугольник делится на 6 равносторонних треугольников. Площадь каждого из треугольников равна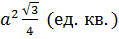 
, значит, площадь правильного шестиугольника равна 
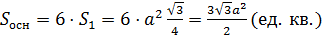. Тогда объём правильной шестиугольной призмы равен 
.
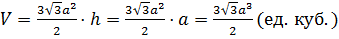Ответ 3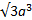 
/2 ед3
№4 Найди объём прямой призмы если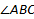 
=120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см2.
Решение: боковая грань прямой призмы является прямоугольником.
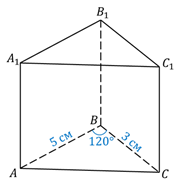
Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.
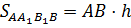
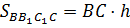
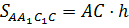
То есть большая боковая грань содержит большую сторону основания.
По условию 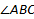=120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.
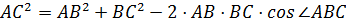
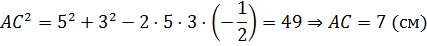
Получим, что длина стороны АС=7см.
Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.
Получим, что длина высоты призмы равна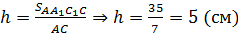 
.
Для нахождения объёма призмы, воспользуемся только что доказанной формулой . Площадь основания можно найти либо по формуле Герона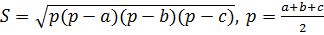 
, либо по формуле 
.
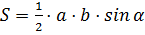Мы воспользуемся второй формулой. Получим, что площадь основания равна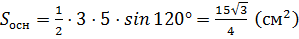 
.
Тогда объём прямой призмы равен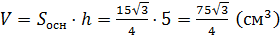 
.
Ответ 75 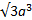/4 см3
№5. Круговой сектор радиуса R с центральным углом 60 градусов вращается вокруг одного из радиусов, образующих этот угол. Найдите объем тела вращения.
Решение:
При вращении кругового сектора АОВ вокруг радиуса ОА получается тело вращения - шаровой сектор радиуса R=ОА и высотой сектора h=DA. Объем его вычисляется по формуле: V= (2/3)*πR²*h. Рассмотрим сечение этого сектора (смотри рисунок): в прямоугольном треугольнике ОВD (радиус круга ОА перпендикулярен хорде ВС) угол ВОD равен 60° (дано). Значит Тогда высота шарового сектора равна h=DA=OA-OD=R-R/2=R/2.
V=(2/3)*π*R²*R/2=(1/3)πR³.
№6. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.
Решение:
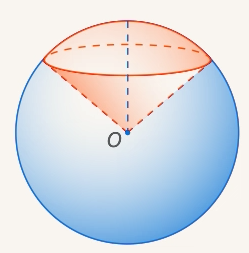
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара. Формула объема шарового сектора: V = (2/3)*πR²*h, где h - высота сегмента. В нашем случае R=H+h, где Н - высота конуса, а h- высота сегмента. Тогда h = R-H = 6-4 =2, так как Н = (1/3)*2*R (дано). Значит V = (2/3)*π*36*2 = 48π.
Ответ: объем шарового сектора равен 48π
№7. По разные стороны от центра шара проведены два параллельных сечения с площадью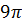 
и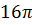 
см2. Расстояние между сечениями равно 
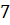см. Определите объём получившегося шарового слоя.
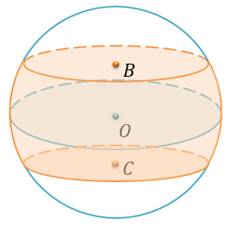
Решение: запишем формулу для вычисления объема шарового слоя.
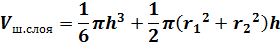
Чтобы найти объём шарового слоя нам необходимо знать его высоту и радиусы двух его оснований.
По условию задачи нам дано расстояние между сечениями, как раз-таки это расстояние и есть высота данного шарового слоя, и она равна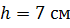 
.
Теперь найдём чему равны радиусы оснований шарового слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга вычисляется по формуле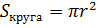 
. Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания равен 
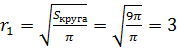(см), радиус второго основания равен 
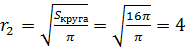(см).
Подставим радиусы оснований и высоту шарового слоя в формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен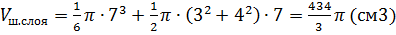 
Домашнее задание
составить конспект (Основные понятия, формулы, рис)
записать задачи
фото прислать на электронную почту техникума kitdisttpop@mail.ua kitdisttpop@mail.ua. или VK https://vk.com/feed с полным названием ФИО студента, группа (например - Иванов И.И., ТПОП-19, Математика)
Срок выполнения до 16.06.20
КРИТЕРИИ ОЦЕНИВАНИЯ
Ответ оценивается отметкой «5», если:
· работа выполнена полностью;
· в логических рассуждениях и обосновании решения нет пробелов и ошибок;
· в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
· работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
· допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
· допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
· допущены существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится в случае:
· полного незнания изученного материала, отсутствия элементарных умений и навыков.
