внутренняя точка x0 области определения f(x) такая что f(x) непрерывна в этой точке, и x0 является одновременно концом интервала строгой выпуклости вверх и концом интервала строгой выпуклости вниз называется точкой перегиба.
Пусть функция 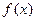 определена и дважды непрерывно-дифференцируема в окрестности точки С. Для того, чтобы (с,
определена и дважды непрерывно-дифференцируема в окрестности точки С. Для того, чтобы (с, 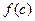 ), была точкой перегиба графика функции
), была точкой перегиба графика функции 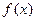 , необходимо чтобы
, необходимо чтобы 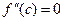 .
.
Дать определение выпуклости графика функции в интервале. Сформулировать достаточное условие выпуклости графика функции
Функция называется выпуклой (или выпуклой вниз) на некотором интервале если для любых двух точек x, y из этого интервала и для любого числа t, принадлежащего отрезку [0,1], выполняется неравенство 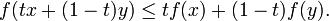
Пусть 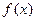 определена и дважды дифференцируема на
определена и дважды дифференцируема на 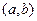 . Для того, чтобы график функции имел направление выпуклости вниз (вверх) достаточно, чтобы
. Для того, чтобы график функции имел направление выпуклости вниз (вверх) достаточно, чтобы 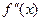 была неотрицательная (неположительная) на
была неотрицательная (неположительная) на 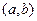 .
.
 2020-08-05
2020-08-05 105
105







