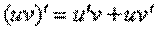
Пример 3
Найти производную функции 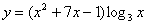
В данной функции содержится сумма 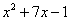 и произведение двух функций – квадратного трехчлена
и произведение двух функций – квадратного трехчлена 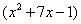 и логарифма
и логарифма 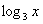 . Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:
. Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:
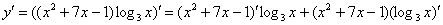
Теперь для скобки 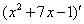 используем два первых правила:
используем два первых правила:
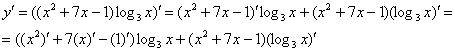
В результате применения правил дифференцирования под штрихами у нас остались только элементарные функции, по таблице производных превращаем их в другие функции. Итоговая запись решения:
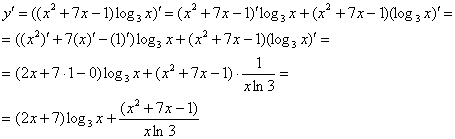
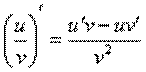
Производная частного функций
Пример 4 Найти производную функции 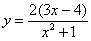
Решаем:
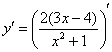
Теперь смотрим на выражение в скобках, как бы его упростить? В данном случае замечаем множитель, который согласно первому правилу целесообразно вынести за знак производной:
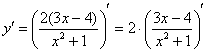
Смотрим на наше выражение в скобках. И здесь – сначала применяем правило дифференцирования частного:
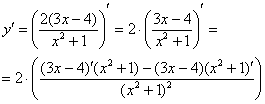
Таким образом, наша страшная производная свелась к производным двух простых выражений. Применяем первое и второе правило, здесь это сделаем устно, надеюсь, Вы уже немного освоились в производных:
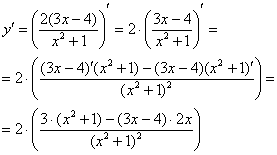
Штрихов больше нет, задание выполнено.
Вот какое решение получается:
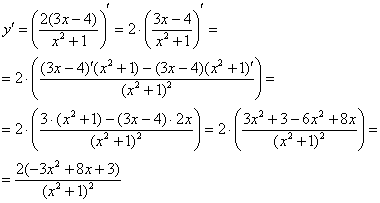
На сегодня остановимся на первых четырех правилах дифференцирования.
Выполните Задания для самостоятельного решения:
Найти производную функции:
1) 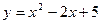
2) f(x) = 3ex – 2x;
3) 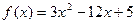
4) у = х5× sinx;
5) у = 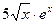
6) y = 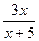 ;
;
7) у = 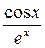 .
.
 2020-08-05
2020-08-05 191
191







