2020-08-05
107
Малое расстояние 
на поверхности 
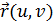в направлении 
может быть найдено по первой квадратичной форме
.
На этом основании первая квадратичная форма поверхности определяет метрику на поверхности. Матрица Грама этой метрики:
,
,
Детерминант метрической формы равен
.
Для любых векторов 
и 
, угол между которыми равен 
, имеем
, 
,
поэтому верно соотношение
.
Перепишем это равенство для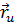 
, 
:
.
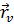Отсюда, используя обозначения (III.4.2), находим:
, 
. (III.5.1)
Вместе с тем, получено
и детерминант первой квадратичной формы есть ее дискриминант.
Длину дуги кривой, проходящей через точку 
в направлении можно вычислить на основании дифференциала дуги 
(III.4.1):
.
Если через точку проходит еще одна линия 
в направлении 
, то угол 
между кривыми 
и 
есть угол между векторами 
и 
и может быть найден из формулы
.
Если первое направление есть направление -линии: 
, 
, второе направление есть направление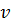 
-линии: 
, 
, и 
угол между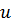 
-линией и 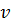-линией, то
.
Выполняется 
.
Элемент площади фигуры на поверхности равен
и по (III.5.1):
.
Теперь площадь фигуры 
, лежащей на поверхности 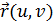, вычисляется по формуле
.
Итак, на основании первой квадратичной формы 
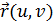(III.4.3) поверхности на поверхности вычисляются длины линий между заданными точками, углы между линиями и площади фигур, лежащих на поверхности, т.е. могут быть произведены все измерения. Форма действительно является метрической.
