2020-08-05
208
В точке 
поверхности 
рассматриваем касательную плоскость 
. Во всех направлениях в точке в 
и в 
к линиям 
на 
проводим касательную прямую 
, она лежит в плоскости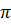 
. Вектор касательной
выписан выше, в п. III.6. В каждом направлении от точки откладывается отрезок
.
В репере 
касательной плоскости 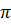обозначим 
. Тогда
.
Так как векторы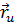 
, 
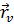неколлинеарны, то
, 
. (III.7.1)
Выражения 
и 
через 
и 
подставим в формулу (III.6.3) нормальной кривизны поверхности
,
откуда получаем
.
Линия, определяемая этим уравнением, называется индикатрисой кривизны в точке или индикатрисой Дюпена, и является центральной линией второго порядка – это либо эллипс, либо две сопряженные гиперболы, либо пара параллельных прямых. Значение детерминанта индикатрисы 
определяет вид индикатрисы.
