III. 8. Классфикация обыкно венных точек поверхности

Точки регулярной поверхности  различаются по виду индикатрисы кривизны поверхности в этих точках. Возможны следующие случаи.

(а).  . Детерминант индикатрисы положителен, индикатриса является эллипсом. Точка  называется эллиптической. Касательная плоскость в точке  имеет с поверхностью одну общую точку - точку ;

(б). . Индикатриса есть пара гипербол. Точка  называется гиперболической. Касательная плоскость 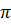 пересекается с поверхностью  по двум прямым - асимптотам гипербол;

(в)  . Индикатриса есть две параллельные прямые. Точка  называется параболической. Касательная плоскость 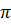 пересекает поверх­ность  по прямой.

(г)  . Индикатриса превращается в точку.  называется точкой уплощения. В этой точке по всем направлениям . Если  - плоскость, то всякая ее точка есть точка уплощения.

Направление на поверхности называется асимптотическим, если нормальная кривизна поверхности в этом направлении равна нулю: . В асимптотическом направлении касательная плоскость к поверхности пе­ресекается с поверхностью по прямой. Из предыдущего видно, что в эл­липтической точке асимптотических точек нет (а), в гиперболической точке имеется два асимптотических направления (б), в параболической точке - одно асимптотическое направление (в); в точке уплощения всякое направление является асимптотическим (г).