Средние показатели анализа ряда динамики

Показатель	Формула расчета	Характеристика показателя
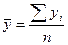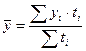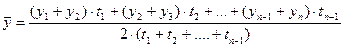
Средний уровень ряда	- интервальный ряд с равноотстоящими уровнями - интервальный ряд с неравноотстоящими уровнями - моментный ряд с равноотстоящими уровнями - моментный ряд с неравноотстоящими уровнями	Показывает усредненную величину изменения ряда динамики.
Средний абсолютный прирост	- по цепной системе 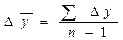- по базисной системе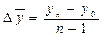	Показывает, на сколько единиц в среднем происходило увеличение (снижение) анализируемого показателя в единицу времени.
Средний коэффициент роста	- по цепной системе 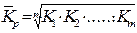- по базисной системе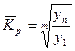	Показывает среднюю относительную скорость изменения уровня явления (в долях единицы – коэффициент роста, в процентах – темп роста).
Средний темп роста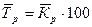
Средний темп прироста		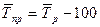Показывает, на сколько процентов произошло увеличение (снижение) показателя в среднем в единицу времени.

где – уровни ряда динамики;

– интервалы времени между смежными датами;

n – число уровней ряда;

m – число коэффициентов роста;

у_n – последний уровень временного ряда;

у₀ – базисный (начальный) уровень ряда.

При анализе рядов динамики необходимо определить общую тенденцию развития. На развитие явления во времени могут оказывать влияние различные факторы, одни из них могут формировать в рядах динамики определенную тенденцию в развитии, другие - оказывают кратковременное воздействие.

При выявлении общей тенденции развития явления применяются различные приемы и методы выравнивания:

а) усреднение по левой и правой половине;

б) укрупнение интервалов;

в) сглаживание рядов динамики на основе скользящих средних;

г) аналитическое выравнивание и др.

Рассмотрим два последних метода.

В основу этого метода положено определение по исходным данным теоретических уровней, в которых случайные колебания погашаются, а основная тенденция развития выражается в виде некоторой плавной линии.

Для выявления тренда в рядах динамики, отображающих развитие за длительный период времени, при вычислении скользящих средних составляются звенья из четного или нечетного числа уровней. Их расчет состоит в нахождении средних величин из уровней ряда с отбрасыванием, при подсчете каждой новой скользящей средней, одного уровня слева (сверху) и присоединением одного уровня справа (снизу).

Например, трехчленная скользящая средняя исчисляется по следующей схеме:

(первая средняя),

(вторая средняя),

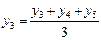(третья средняя) и т.д.

При четном числе уровней каждое значение скользящей средней приходится на промежуток между двумя смежными уровнями. Так, первая скользящая средняя записывается между вторым и третьим, вторая - между третьим и четвертым уровнями и т. д. (таблица 9).

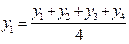(первая средняя),

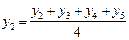(вторая средняя),

(третья средняя) и т.д.

Для третьего уровня устанавливается серединное значение между первой и второй скользящими средними, для четвертого центрируются вторая и третья скользящие средние и т. д.

Если при сглаживании рядов динамики звенья скользящей составляются из нечетного числа уровней, то необходимость в центрировании отпадает.

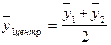(1-й сглаженный средний уровень),

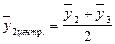(2-й сглаженный средний уровень)

(3-й сглаженный средний уровень) и т.д.

Рассмотрим методику скользящей средней на примере.

Таблица 8

Имеются данные о производстве деталей на заводе, тыс. штук.

Месяц	у	Четырехчленные скользящие
		средние не центрированные	средние центрированные
январь	15,3
февраль	16,8
		16,4
март	16,4		16,6
		16,9
апрель	16,9		16,9
		16,9
май	17,5		17,0
		17,1
июнь	16,9		17,2
		17,3
июль	17,1		17,2
		17,1
август	17,5		17,2
		17,4
сентябрь	16,9		17,5
		17,7
октябрь	17,9		17,8
		18,0
ноябрь	18,5

декабрь	18,6

Центрированные средние наносят на график с эмпирическими данными.

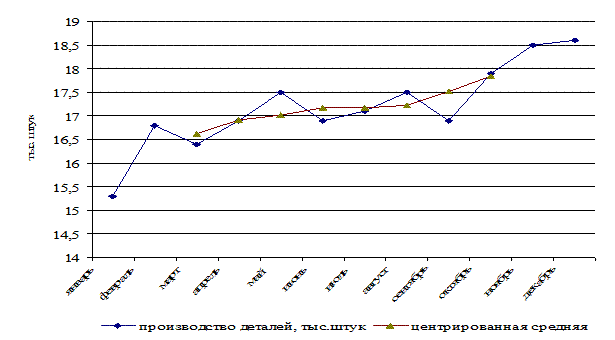
Рис. 3. Динамика производства деталей на заводе, тыс. штук

Особенность способа сглаживания рядов динамики на основе скользящих средних заключается в том, что полученные средние не дают теоретических рядов, в основе которых лежала бы определенная математическая закономерность.

Более совершенным приемом изучения общей тенденции в рядах динамики является аналитическое выравнивание. Оно основано на допущении, что изменения в рядах динамики могут быть выражены определенным математическим законом. На основе теоретического анализа выявляется характер явления во времени и на этой основе выбирается то или иное математическое выражение типа закономерности изменения явления:

- линейная функция

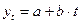
- полином второго порядка

- полином третьего порядка

- степенная функция

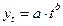
- показательная функция

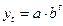
и другие.

Данный прием сводится к следующему:

а) на основе экономического анализа явления за рассматриваемый период времени выявляется его характер;

б) исходя из характера явления выбирается то или иное математическое уравнение;

в) определяются параметры уравнения;

г) рассчитываются теоретические (выровненные) уровни ряда динамики, которые наносятся на график эмпирических значений;

д) прогнозируются уровни динамического ряда на основе аппроксимирующей модели на предстоящий период.

Рассмотрим выравнивание ряда динамики, используя линейную функцию (таблица 9). Задача аналитического выравнивания решается с помощью метода наименьших квадратов, смысл которого состоит в том, что вычисленная линия теоретических уровней должна проходить в максимальной близости к фактическим уровням ряда, то есть

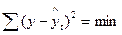
где y – исходные (эмпирические) уровни динамического ряда;

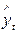– расчетные (теоретические) уровни ряда динамики.

Выравнивание с использованием линейной функции осуществляется по формуле:

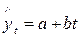
где y – исходные (эмпирические) уровни ряда динамики

a и b – параметры уравнения,

t – время

Параметры уравнения находятся на основе системы уравнений:

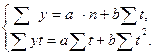
Расчет параметров заметно упрощается, если перенести начало отсчета времени в середину исходного ряда (что бы 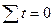). Причем, если число уровней ряда нечетное, нумерация t следующая: …-3, -2, -1, 0, +1, +2, +3….; а если число уровней ряда четное, нумерация t будет следующая: …-5, -3, -1, +1, +3, +5….

При условии, что St=0 (графа В таблицы 9) исходные нормальные уравнения принимают вид:

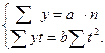отсюда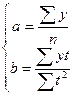

Необходимые величины рассчитаны в графах Г и Д таблицы 9.

Параметризованное уравнение имеет вид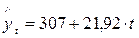

В полученное параметризованное уравнение подставляют значения t и получают теоретические значения исследуемого признака 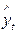(графа Е таблицы 9), которые и являются тенденцией данного явления. Их наносят на график с эмпирическими данными (рис. 4).