Вiльнi коливання матерiальної точки при наявностi опору

 

При невеликих швидкостях сила опору середовища прямо пропорцiональна швидкостi i напрямлена протилежно їй. Проекцiя сили опору на вiсь Ох дорівнює R_x=- 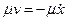  (μ >0; знак ”мiнус” тому, що сила опору напрямлена протилежно до швидкостi). Коефiцiєнт μ дорiвнює силi опору при швидкостi руху точки, рiвнiй одиницi. Якщо на матерiальну точку дiють сила опору R_x = -  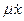i пружна сила F = - 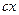, то рiвняння руху буде таким:

m  =-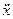

або

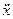+ 2 n 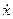+ 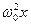= 0,                         (5.10)

де n = μ/ 2 m - показник затухання, μ - коефiцiєнт в’язкого опору, 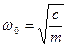 - циклiчна частота власних коливань.

Одиниця вимiрювання показника затухання n – с^-1.

Для вiдповiдного характеристичного рiвняння маємо коренi:

;

а)  у випадку, коли n < ω ₀ (сила опору досить мала) загальний розв’язок рiвняння (5.10) має вигляд:

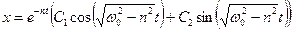   (5.11)

або

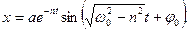.               (5.12)

Рiвняння (5.12) показує, що амплiтуда ae^-nt коливань з часом зменшується. Такi коливання називаються затухаючими коливаннями, рiвняння (5.12) називають рiвнянням затухаючих коливань.

Циклiчна частота затухаючих коливань дорiвнює

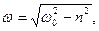                            (5.13)

перiод затухаючих коливань дорiвнює

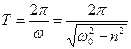.                       (5.14)

Ця формула доводить, що поява сил опору збiльшує перiод коливань. З погляду фiзики це зрозумiло: опiр уповiльнює рух. Сталi iнтегрування а i φ ₀ обчислюють за формулами:    

 

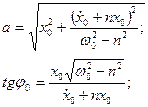
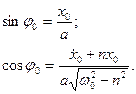                                                         (5.15)

Вiдношення двох послiдовних максимальних вiдхилень дорівнює:

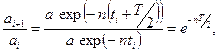          (5.16)

де Т визначається формулою (5.14). Величина Δ = е^{-nT/ 2} називається декрементом затухання; натуральний логарифм декремента, тобто величина - nТ/ 2, називається логарифмiчним декрементом затухання:

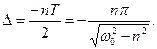                  (5.17)

Декремент затухання характеризує швидкiсть затухання амплiтуди коливання;

б)  у випадку, коли n > ω ₀ (сила опору досить велика), коренi Z ₁ i Z ₂ дiйснi i рiзнi:

.

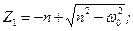
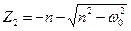Загальний розв’язок рiвняння (5.10) в цьому випадку такий:

            (5.18)

або

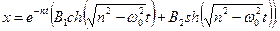  (5.19)

де

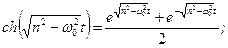
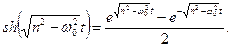
В деяких випадках розв’язок (5.19) можна подати у виглядi:

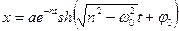;              (5.20)

змiщення х асимптотичнo прямує до нуля, коли t →∞. При досить великiй силi опору рух не є коливальним. Такий рух називають аперiодичним затуханням;

  в) у випадку, коли n = ω ₀ (особливий випадок), корені Z ₁ і Z ₂ однакові та від’ємні Z ₁= Z ₂= - n і загальний розв’язок рiвняння (5.10) такий:

x = e^-nt (C ₁ t + C ₂).                          (5.21)

Вiдповiдний рух зводиться до аперiодичного затухання.

На використаннi закономiрностей затухаючих коливань працюють демпфери, що бувають рiзних систем i вiдiграють роль глушителiв шкiдливих механiчних i електричних коливань.

 

Зауваження. Для закріплення матеріалу §5 (пунктів 5.1 і 5.2) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 32.1, 32.2, 32.5, 32.6, 32.12, 32.15, 32.24, 32.26, 32.28, 32.60, 32.70, 32.77;

2) № 32.4, 32.13, 32.14, 32.16, 32.18, 32.30, 32.36, 32.53, 32.59, 32.65, 32.66, 32.68, 32.69, 32.71;

3) №32.38, 32.41, 32.43, 32.46, 32.49, 32.74, 32.75, 32.76.

Рекомендується розв’язати також задачі № 659, 660, 669, 672, 674 зі збірника “Сборник задач по теоретической механике /Под ред. М. А. Бражниченко. – М., Высшая школа, 1986”.