2020-08-05
753
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома)
Пусть, например, мы хотим разложить силу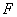 
на две составляющие, лежащие в одной плоскости с 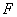и направленные вдоль прямых АВ и АС. Для этого достаточно из конца вектора, изображающего силу 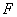, провести две прямые, параллельные АВ и АС. Отрезк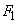и 
и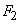 
изобразят искомые силы.
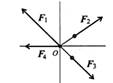
Вопрос 4
Определение равнодействующей системы сил геометрическим способом. Силовой многоугольник
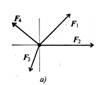Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил. Вектор равнодействующей силы соединит начало первого вектора с концом последнего.
Вектор равнодействующей направлен навстречу векторам сил слагаемых. Такой способ получения равнодействующей называют геометрическим.
|
|
|
Порядок построения многоугольника сил:
Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпадал с началом последующего.
Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец Последнего вектора должен совпасть с началом первого.
