Одномерным называется движение системы с одной степенью свободы: 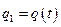 . в самом общем виде функция Лагранжа выглядит так:
. в самом общем виде функция Лагранжа выглядит так:
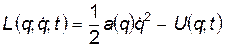 (1)
(1)
Величина 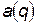 - некоторая функция обобщенной координаты
- некоторая функция обобщенной координаты 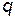 . Уравнение Лагранжа и начальные условия имеют вид:
. Уравнение Лагранжа и начальные условия имеют вид:
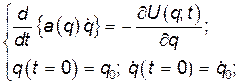 (2)
(2)
В общем виде, при произвольной потенциальной энергии 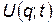 , зависящей как от координаты
, зависящей как от координаты 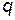 , так и от времени
, так и от времени 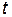 , уравнения Лагранжа (2) аналитически не решаются. Ситуация радикально упрощается, когда потенциальная энергия не зависит явно от времени, т.е.
, уравнения Лагранжа (2) аналитически не решаются. Ситуация радикально упрощается, когда потенциальная энергия не зависит явно от времени, т.е.
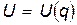 (3)
(3)
Отличительной чертой стационарного одномерного движения является то обстоятельство, что решение уравнения (2) легко находится в общем виде при произвольной зависимости 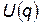 , по крайней мере в квадратурах.
, по крайней мере в квадратурах.
Т.к. в этом случае 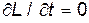 , то
, то 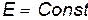 и для нахождения закона движения частицы проще всего воспользоваться законом сохранения энергии:
и для нахождения закона движения частицы проще всего воспользоваться законом сохранения энергии:
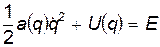 (4)
(4)
Из уравнения (5.4) находим, что
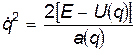 ;
; 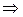
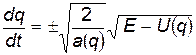 .
.
Это уравнение первого порядка с разделяющимися переменными:
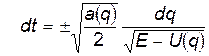 (5)
(5)
Его общее решение имеет вид:
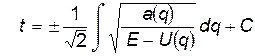 (6)
(6)
Решение уравнения (6) можно также записать в виде:
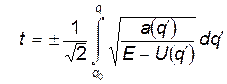 (7)
(7)
Если интеграл в формулах (7) удастся вычислить аналитически, то мы получим зависимость 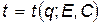 , т.е. закон движения в неявном виде. Если это уравнение удастся ещё и разрешить относительно обобщенной координаты
, т.е. закон движения в неявном виде. Если это уравнение удастся ещё и разрешить относительно обобщенной координаты 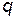 , то мы получим закон движения частицы в явном виде:
, то мы получим закон движения частицы в явном виде: 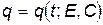 и задача будет полностью завершена.
и задача будет полностью завершена.
Роль двух произвольных постоянных в формуле (6) играют полная энергия 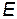 и произвольная константа
и произвольная константа 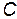 . Если величина
. Если величина 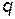 есть обычная декартова координата
есть обычная декартова координата 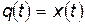 , то величина
, то величина 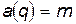 - масса частицы. В этом случае все полученные выше формулы будут выглядеть так:
- масса частицы. В этом случае все полученные выше формулы будут выглядеть так:
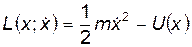 (8)
(8)
Уравнение Лагранжа сводится ко второму закону Ньютона:
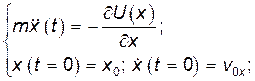 (9)
(9)
Закон сохранения энергии теперь выглядит совсем привычным образом:
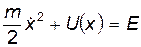 (10)
(10)
Отсюда находим, что
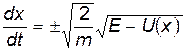 , т.е.
, т.е. 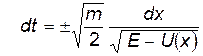 (11)
(11)
так, что
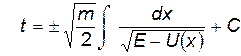 (12)
(12)
Решение уравнения (11) можно также записать в виде:
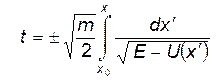 (13)
(13)
Здесь
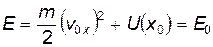 (14)
(14)
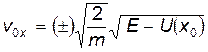 (15)
(15)
Поскольку кинетическая энергия всегдаположительная величина, то из закона сохранения энергии 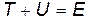 следует, что движение частицы может происходить только в тех областях пространства, где
следует, что движение частицы может происходить только в тех областях пространства, где
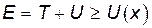 (16)
(16)
Неравенство (16) определяют границы области движения частицы. корни уравнения
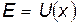 (17)
(17)
определяют истинные точки остановки частицы. В этих точках 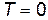 и, следовательно,
и, следовательно, 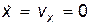 .
.
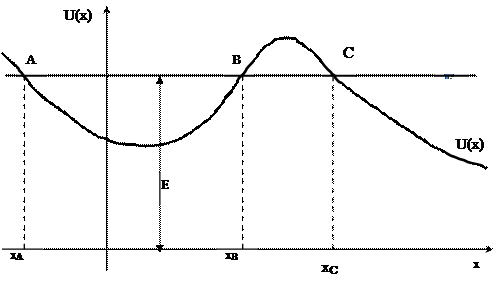 Если область движения ограничена двумя точками остановки, то движение происходит между этими точками в ограниченной области пространства. такое движение называется финитным движением. Если же область движения ограничена с одной стороны одной точкой остановки (или вообще не ограничена), то такое движение называется инфинитным. При инфинитном движении частица уходит на бесконечность. Рассмотрим, например, зависимость
Если область движения ограничена двумя точками остановки, то движение происходит между этими точками в ограниченной области пространства. такое движение называется финитным движением. Если же область движения ограничена с одной стороны одной точкой остановки (или вообще не ограничена), то такое движение называется инфинитным. При инфинитном движении частица уходит на бесконечность. Рассмотрим, например, зависимость 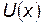 , изображенную на рисунке. Проведя на этом рисунке горизонтальную прямую, соответствующую заданному значению полной энергии
, изображенную на рисунке. Проведя на этом рисунке горизонтальную прямую, соответствующую заданному значению полной энергии 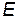 , можно сразу определить точки остановки
, можно сразу определить точки остановки 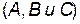 и области доступного движения.
и области доступного движения.
На нашем рисунке область доступного финитного движения, это движение в «потенциальной яме» 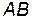 , между точками остановки
, между точками остановки 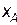 и
и 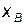 . Область доступного инфинитного движения это область
. Область доступного инфинитного движения это область 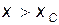 . достигнув точки
. достигнув точки 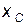 , частица останавливается. в точке
, частица останавливается. в точке 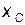 на частицу действует сила
на частицу действует сила 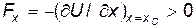 , которая заставляет изменить направление движения частицы и частица тут же начинает двигаться вправо, в область
, которая заставляет изменить направление движения частицы и частица тут же начинает двигаться вправо, в область 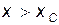 .
.
 2020-08-05
2020-08-05 559
559








