Определим теперь вид функции Лагранжа для одной свободной частицы. Как показано выше, в этом случае 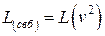 . При этом уравнения движения во всех инерциальных отчетах должны иметь один и тот же вид.
. При этом уравнения движения во всех инерциальных отчетах должны иметь один и тот же вид.
Пусть система 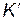 движется относительно
движется относительно 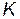 с постоянной скоростью
с постоянной скоростью 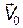 . Тогда функция Лагранжа
. Тогда функция Лагранжа 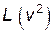 в системе
в системе 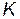 должна перейти в такую функцию
должна перейти в такую функцию 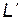 в системе
в системе 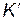 , которая, если и отличается от функции
, которая, если и отличается от функции 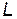 , то лишь на полную производную какой-то функции координат и времени. Поскольку
, то лишь на полную производную какой-то функции координат и времени. Поскольку 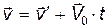 , то
, то
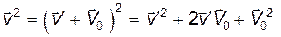 , т.е.
, т.е. 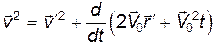 (7)
(7)
Учитывая это, сразу получаем, что для свободной частицы ф. Лагранжа должна быть пропорциональна квадрату скорости:
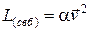 (8)
(8)
Уравнение Лагранжа для свободной частицы теперь будет выглядеть так:
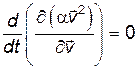 , т.е.
, т.е. 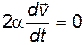
Сравнивая это с уравнением второго закона Ньютона для свободной частицы 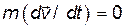 , находим, что
, находим, что 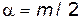 . Здесь
. Здесь 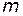 - инертная масса тела. Таким образом, окончательно получаем следующее выражение для функции Лагранжа одной свободной частицы:
- инертная масса тела. Таким образом, окончательно получаем следующее выражение для функции Лагранжа одной свободной частицы:
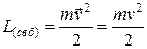 (9)
(9)
Отметим, что в этом пункте мы существенно воспользовались вторым законом Ньютона. Иначе мы не смогли бы понять, что есть 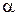 .
.
Если механическая система состоит не из одной, а из 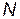 невзаимодействующих частиц, то в силу свойства аддитивности функции Лагранжа, получим
невзаимодействующих частиц, то в силу свойства аддитивности функции Лагранжа, получим
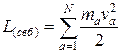 (10)
(10)
Величина
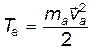 (11)
(11)
называется кинетическойэнергией 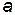 - ой частицы.
- ой частицы.
Сумма кинетических энергий всех частиц есть полная кинетическая энергия системы:
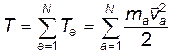 (12)
(12)
Таким образом, кинетическая энергия есть величина аддитивная.
Рассмотрим теперь систему 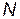 м.т., взаимодействующих только друг с другом, но ни с какими посторонними телами, не входящими в эту систему. Такая система называется замкнутой системой.
м.т., взаимодействующих только друг с другом, но ни с какими посторонними телами, не входящими в эту систему. Такая система называется замкнутой системой.
Оказывается, что в классической механике, когда скорости частиц малы по сравнению со скоростью света 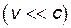 , взаимодействие между точками системы может быть описано прибавлением к функции Лагранжа невзаимодействующих точек, некоторой функции координат
, взаимодействие между точками системы может быть описано прибавлением к функции Лагранжа невзаимодействующих точек, некоторой функции координат 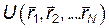 . Конкретный вид этой функции зависит от характера взаимодействия между частицами. Величина
. Конкретный вид этой функции зависит от характера взаимодействия между частицами. Величина 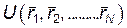 называется потенциальной энергией системы. С учетом сказанного, в самом общем виде, ф. Лагранжа для замкнутой системы из
называется потенциальной энергией системы. С учетом сказанного, в самом общем виде, ф. Лагранжа для замкнутой системы из 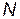 м.т. в декартовой системе координат будет выглядеть так:
м.т. в декартовой системе координат будет выглядеть так:
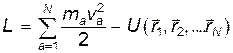 (13)
(13)
Потенциальная энергия зависит от положения всех м.т. 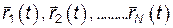 в один и тот же момент времени
в один и тот же момент времени 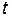 . Это означает, что изменение положения хотя бы одной из них, мгновенно отражается на всех остальных. Следовательно, в классической механике считается, что взаимодействие между телами «распространяется» мгновенно, с бесконечно большой скоростью.
. Это означает, что изменение положения хотя бы одной из них, мгновенно отражается на всех остальных. Следовательно, в классической механике считается, что взаимодействие между телами «распространяется» мгновенно, с бесконечно большой скоростью.
Зная функцию Лагранжа, можем записать систему уравнений Лагранжа в следующем символическом векторном виде:
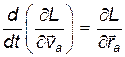 ,
, 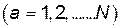 (14)
(14)
Поскольку 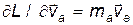 , а
, а 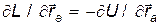 , то система уравнений (14) примет вид:
, то система уравнений (14) примет вид:
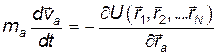 ,
,  (15)
(15)
Вектор
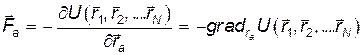 (16)
(16)
называется силой, действующей на 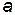 -ю частицу, со стороны всех остальных частиц системы. Вместе с
-ю частицу, со стороны всех остальных частиц системы. Вместе с 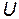 сила зависит только от координат частиц, но не от их скоростей:
сила зависит только от координат частиц, но не от их скоростей: 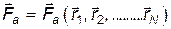 . Теперь система уравнений Лагранжа запишется так:
. Теперь система уравнений Лагранжа запишется так:
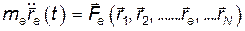 (17)
(17)
Таким образом, если в качестве обобщенных координат выбрать декартовы координаты, уравнения Лагранжа сводятся к системе уравнений второго закона Ньютона.
При решении большинства задач, оказывается удобным использовать не декартовы, а некоторые обобщенные координаты 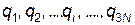 . В этом случае для написания функции. Лагранжа нужно произвести соответствующие преобразования. Прежде всего, нужно выразить все декартовы координаты точек через обобщенные координаты
. В этом случае для написания функции. Лагранжа нужно произвести соответствующие преобразования. Прежде всего, нужно выразить все декартовы координаты точек через обобщенные координаты 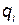
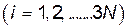 :
:
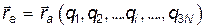 .
.
Затем нужно выразить кинетическую энергию системы через выбранные обобщенныекоординаты. Т.к.
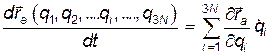 ,
,
то
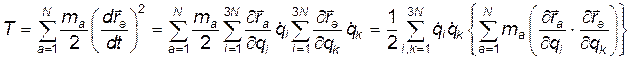
Обозначим
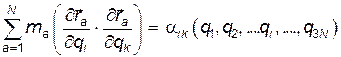 (18)
(18)
Отсюда видно, что матрица 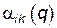 зависит только от обобщенных координат и является симметричной матрицей. Таким образом, в обобщенных координатах кинетическая энергия системы по-прежнему является квадратичной функцией скоростей, но может зависеть и от обобщенных координат:
зависит только от обобщенных координат и является симметричной матрицей. Таким образом, в обобщенных координатах кинетическая энергия системы по-прежнему является квадратичной функцией скоростей, но может зависеть и от обобщенных координат:
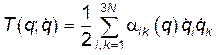 .
.
Теперь функцию Лагранжа запишем в виде:
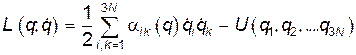 (19)
(19)
 2020-08-05
2020-08-05 762
762








