Кинематика и динамика упругого столкновения частиц. Переход в Ц-систему. Импульсные диаграммы. Связь углов рассеяния в Л- и Ц-системах

 

       Столкновение двух частиц называется упругим, если оно не сопровождается изменением их внутреннего состояния, в том числе не изменяется их внутренняя энергия. Термин "столкновение" предполагает, что взаимодействие между частицами происходит в течение какого-то ограниченного времени, после чего частицы движутся как свободные.

Процесс упругого столкновения можно проанализировать в рамках законов сохранения энергии и импульса. Эти результаты получались и подробно исследовались в курсе общей физики. Здесь мы интерпретируем их графически с помощью так называемых импульсных диаграмм. Ограничимся подробным рассмотрением простого, но важного и часто встречающегося случая, когда вторая частица до столкновения покоилась (в общем случае формулы очень громоздки), т.е.

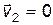,                                                                    (1)

В этом случае импульс системы и относительный импульс определяются импульсом первого тела

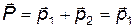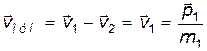  и                         (2)

Тогда импульсы те в системе центра инерции до и после столкновения равны:

,                                                (3)

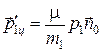,                                         (4)

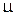(  - приведенная масса). Кинетическая энергия в Ц-системе

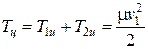                                                    (5)

Тогда формулы для импульсов тел в Л-системе после столкновения можно записать в виде:

                            (6)

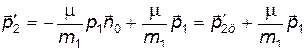                         (7)

Рассмотрим три случая, которые отличаются друг от друга соотношением масс частиц 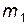 и .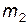

1. Налетающая частица  легче покоящейся частицы 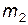, т.е.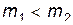

Проведем следующие построения (См. рисунок). Отложим отрезок 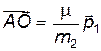. Из точки 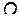отложим отрезок . Тогда очевидно, что отрезок 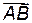 будет представлять собой импульс налетающей частицы до столкновения: . Из точки  проведем окружность радиусом 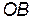. Точка  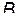будет лежать на этой окружности, а точка  будет находиться внутри круга, т.к. при 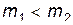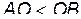. Заметим, что отрезок 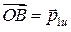, т.е. одновременно представляет собой импульс налетающей частицы в Ц - системе.

Рассмотрим на окружности произвольную точку . Отрезок  можно рассматривать как импульс первой частицы после столкновения в Ц - системе: 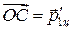, т.к. . Следовательно, угол  есть угол поворота первой частицы в Ц – системе. Тогда отрезок 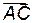 есть импульс первой частицы после столкновения в Л – системе: .

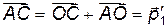Одновременно, 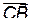 есть импульс второй частицы после столкновения в Л – системе: 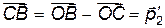. Т.о. на одной векторной диаграмме удается одновременнопредставить векторы импульсов частиц до и после столкновений как в Л – системе, так и в Ц – системе. Именно это обстоятельство делает векторные импульсные диаграммы исключительно наглядными и позволяет установить из них связь между различными величинами в Л – и в Ц – системах. Например, из диаграммы сразу видно, что угол отклонения  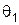первой частицы в Л – системе может изменяться во всем интервале 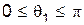, а угол отклонения  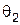второй частицы в Л – системе может изменяться в интервале 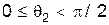. Видно, что 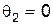, когда 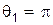, что имеет место при 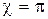. При этом частицы разлетаются в разныестороны вдоль одной прямой: 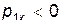, а . Это соответствует "лобовому" столкновению частиц. При 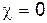, 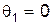. При этом , а . 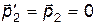Это соответствует отсутствию столкновения частиц.

Установим связь между углами отклонения частиц 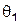 и 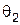 в Л – системе и углом поворота  в Ц – системе. Углы 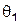 и 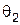 представляют собой углы отклонения частиц после столкновения по отношению к направлению удара, т.е. по отношению к вектору налетающей частицы 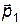, т.е. по отношению к отрезку  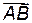на рисунке.

Сначала установим связь между углам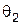и  и . Поскольку треугольник 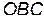 равнобедренный, то . Отсюда сразу получаем, что

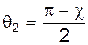                                                                   (8)

Теперь установим связь между углам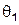и  и . Из рисунка следуют соотношения:

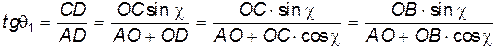
Поскольку 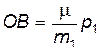, а 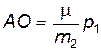, то получаем

.

Эту формулу обычно записывают в виде:

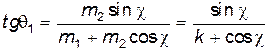                                  (9)

Угол , т.к. точка  лежит внутри круга. Поскольку 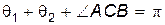, то при  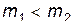угол разлета частиц  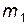и 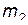 после столкновения меньше чем :

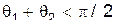,                                            (10)

Рассмотрим случай "лобового" удара. Из диаграммы 1 видно, что в этом случае налетающая частица 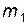 полетит в сторону, противоположную её начальному направлению движения: 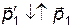. Точка  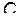будет находиться на одном диаметре окружности слева от точки . Т.е. при "лобовом" столкновении 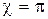. Поэтому

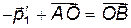, т.е.  ,

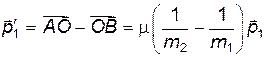т.е.

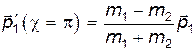                                                    (11)

Следовательно

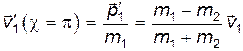                                        (12)

Для покоящейся частицы при "лобовом" ударе , т.е.

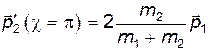                                                 (13)

Следовательно,

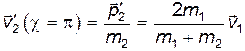                                        (14)

Если частица 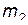 до столкновения покоилась, то наибольшую энергию, которую может потерять налетающая частица, будет равна энергии, приобретенной второй частицей именно после "лобового" столкновения:

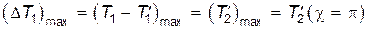                     (15)

Используя формулу (15) легко получаем:

(16)

Здесь 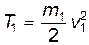 - первоначальная энергия налетающей частицы.

Рассмотрим случай, когда налетающая частица 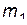 тяжелее покоящейся частицы , т.е. 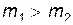. В этом случае построение векторной импульсной диаграммы производится аналогично тому, как это делалось выше для случая 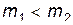. Отличие будет состоять только в том, что теперь точка  будет лежать вне круга радиуса 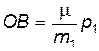, т.к. длина отрезка  будет больше 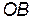, поскольку  (рис.10.6).

Такое, казалось бы, не столь большое отличие, приводит, однако, к существенному изменению результата взаимодействия частиц, по сравнению с рассмотренным выше случаем 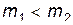. В то время, как при  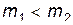скорость первой частицы после столкновения могла иметь любоенаправление 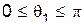, теперь угол отклонения налетающей частицы  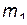не может превышать некоторого максимального значения 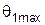, так, что при  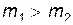 величина  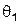может изменяться в пределах: . 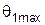Значение угла  может легко определено из векторной диаграммы 2. Максимальному отклонению первой частицы в Л – системе соответствует такое положение точки 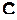, при котором прямая AС касается окружности в точке E.

Поскольку треугольник AEO – прямоугольный, то .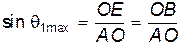

Поскольку 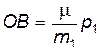, а 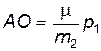, то сразу получаем, что

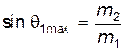                                                          (17)

Значению угла 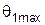 соответствует угол поворота в Ц – системе , так, что .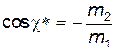

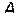обсудим значение угла разлета. Теперь угол , т.к. точка  лежит вне круга. Поскольку 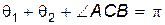, то при  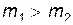угол разлета частиц  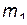и  после столкновения больше чем :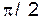

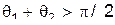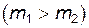,                                            (18)

Кроме того, как это видно из диаграммы 2, одному и тому же значению угла  будет соответствовать два различных значения угла 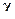 в Ц – системе, т.к. прямая AC пересекает окружность в двух точках. Но это означает, что одному и тому же углу отклонения  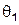будет соответствовать две различные пары значений импульсов  и 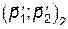. Кроме того, одному и тому же углу отклонения  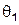будет соответствовать два различных значения угла .

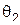Пусть теперь налетающая ипокоящаяся частицы имеют одинаковую массу, т.е. , так, что 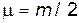. В этом случае векторная диаграмма имеет наиболее простой вид, т.к. отрезк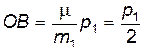и  и 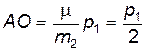 оказываются равными. Поэтому точк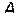и  и 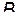 будут лежать на противоположных концах диаметра (рис.3). B этом случае треугольник  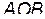является равнобедренным. Поэтому . Следовательно, в случае частиц равных масс получаем:

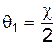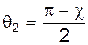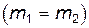;         ;                                 (19)

Формула (19) для угла 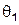 получается конечно из общей формулы, если в ней положить :

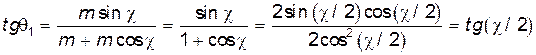
Одинаковые частицы всегда разлетаются под прямым углом друг к другу. Это видно как из диаграммы 3, так и непосредственно из формул (19):

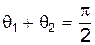                                                                             (20)

16.Дифференциальное сечение рассеяния частиц.