Формула Резерфорда
19 Малые одномерные колебания (свободные и вынужденные).
20
21
22
23
24 Малые колебания системы со многими степенями свободы. Собственные частоты и нормальные координаты
Рассмотрим случай малых колебаний системы частиц, имеющей 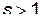 степеней свободы. Самый общий вид функции Лагранжа такой системы таков:
степеней свободы. Самый общий вид функции Лагранжа такой системы таков:
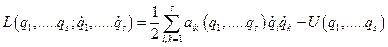 (1)
(1)
 (2)
(2)
Устойчивому положению равновесия соответствует такое состояние системы, в котором её потенциальная энергия 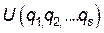 имеет минимум. Малые отклонения от положения равновесия приводят к возникновению сил, которые стремятся вернуть систему обратно в состояние равновесия. Пусть
имеет минимум. Малые отклонения от положения равновесия приводят к возникновению сил, которые стремятся вернуть систему обратно в состояние равновесия. Пусть 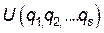 имеет минимум при
имеет минимум при 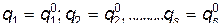 . При малых отклонениях от положения равновесия потенциальную энергию
. При малых отклонениях от положения равновесия потенциальную энергию 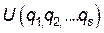 можно разложить в ряд Тейлора по величинам разности
можно разложить в ряд Тейлора по величинам разности
 ,
, 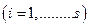 (3)
(3)
которые представляют собой малые отклонения от положения равновесия системы. Ограничимся в этом разложении членами второго порядка малости:
 (4)
(4)
Примем за начало отсчета потенциальной энергии её значение в минимуме, т.е. будем считать, что 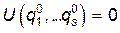 . В точке минимума
. В точке минимума
 (5)
(5)
Обозначим
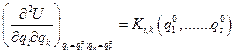 ,
, 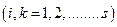 (6)
(6)
Из (6) следует, что коэффициенты 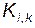 симметричны относительно перестановки индексов:
симметричны относительно перестановки индексов:
 (7)
(7)
С учетом всего сказанного, выражение для потенциальной энергии (4) для потенциальной энергии вблизи положения равновесия  принимает простой вид:
принимает простой вид:
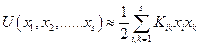 (8)
(8)
Теперь упростим выражение для кинетической энергии в функции Лагранжа (15.2). Поскольку величины 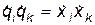 уже являются величинами второго порядка малости, то в силу малости отклонения от положения равновесия, в рамках рассматриваемой точности можно считать, что
уже являются величинами второго порядка малости, то в силу малости отклонения от положения равновесия, в рамках рассматриваемой точности можно считать, что
 (9)
(9)
Постоянные коэффициенты 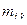 , так же как и величины
, так же как и величины 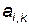 симметрии величины относительно перестановки индексов:
симметрии величины относительно перестановки индексов: 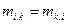 . С учетом всего сказанного функция Лагранжа (1) будет выглядеть так:
. С учетом всего сказанного функция Лагранжа (1) будет выглядеть так:
 (10)
(10)
Теперь запишем систему  уравнений Лагранжа для функции Лагранжа (10):
уравнений Лагранжа для функции Лагранжа (10):
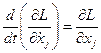 ;
; 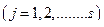 (11)
(11)
Вычисляя производные 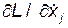 и
и 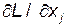 :
:
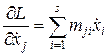 (12)
(12)
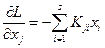 (13)
(13)
и подставляя их в уравнения Лагранжа, получаем:
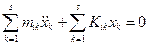 ,
, 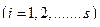 (14)
(14)
Здесь мы переобозначили индексы суммирования 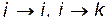 , чтобы уравнения движения имели более привычный вид. Или в развернутом виде:
, чтобы уравнения движения имели более привычный вид. Или в развернутом виде:
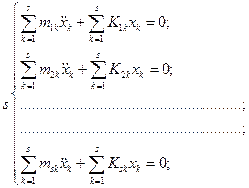 (15)
(15)
Система дифференциальных уравнений (15) и есть уравнения движения для малых колебаний системы с  степенями свободы для величин
степенями свободы для величин 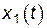 ,
, 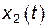 ,…….
,……. 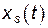 .
.
Ищем решение системы в комплексном виде:
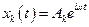 (16)
(16)
Здесь 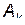 некоторые, пока неизвестные комплексные постоянные:
некоторые, пока неизвестные комплексные постоянные: 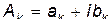 . Подставляя (16) в систему уравнений (15), получаем после сокращения на общий множитель
. Подставляя (16) в систему уравнений (15), получаем после сокращения на общий множитель 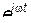 систему линейных однородных алгебраических уравнений, которым должны удовлетворять постоянные
систему линейных однородных алгебраических уравнений, которым должны удовлетворять постоянные 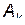 :
:
 ;,
;, 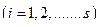 (17)
(17)
Для того, чтобы эта система однородных уравнений имела отличные от нуля решения, необходимо, чтобы её определитель обращался в ноль:
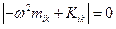 ,
, 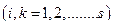 (18)
(18)
(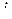 - номер строки;
- номер строки;  - номер столбца).
- номер столбца).
Уравнение (18) называется характеристическим уравнением. Оно представляет собой алгебраическое уравнение порядка  относительно величин
относительно величин 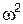 . В общем случае оно имеет
. В общем случае оно имеет  различных и положительных корней:
различных и положительных корней: 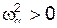 , где
, где 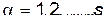 . Определенные из уравнения (18) величины
. Определенные из уравнения (18) величины 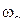 называются собственными частотами системы.
называются собственными частотами системы.
Согласно уравнению (18), собственные частоты колебаний полностью определяется только свойствами механической системы (коэффициентами 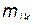 и
и 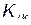 ), и не зависят от начальных условий (и соответственно от амплитуд колебаний).
), и не зависят от начальных условий (и соответственно от амплитуд колебаний).
После того, когда все собственные частоты 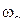 определены, можно частично определить значения коэффициентов
определены, можно частично определить значения коэффициентов 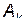 . Если все частоты различны, то значения величин
. Если все частоты различны, то значения величин 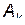 пропорциональны минорам определителя (15.21), в котором нужно заменить
пропорциональны минорам определителя (15.21), в котором нужно заменить 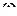 на величину
на величину 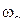 . Каждому значению координаты
. Каждому значению координаты 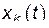 будет соответствовать свой минор
будет соответствовать свой минор 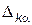 :
:
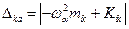 (19)
(19)
(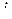 - номер строки;
- номер строки; 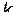 - номер столбца). Тогда частное решение будет иметь вид:
- номер столбца). Тогда частное решение будет иметь вид:
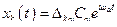 ,
, 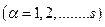 . (20)
. (20)
Здесь  - произвольные комплексные постоянные.
- произвольные комплексные постоянные.
Общее решение системы уравнений (15) есть суперпозиция частных решений (20). Переходя как обычно к вещественной части общее решение можно записать в виде (миноры 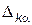 величины действительные):
величины действительные):
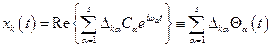 ,
, 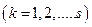 (21)
(21)
Здесь обозначено
 (22)
(22)
Общее решение (21) содержит 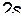 неизвестных постоянных
неизвестных постоянных 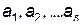 и
и 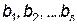 . Эти постоянные определяются из начальных условий:
. Эти постоянные определяются из начальных условий:
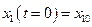 ;
; 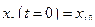 ;
; 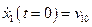 ;
;  (23)
(23)
Из формулы (23) видно, что изменение каждой из координат 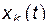 со временем представляет собой наложение
со временем представляет собой наложение  простых гармонических колебаний
простых гармонических колебаний 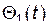 ,
,  ,…….
,……. 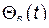 с произвольными амплитудами и фазами (которые определяются из начальных условий), но имеющих вполне определенные частоты
с произвольными амплитудами и фазами (которые определяются из начальных условий), но имеющих вполне определенные частоты 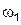 ,
, 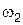 ,…….
,……. 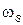 , которые от начальных условий не зависят.
, которые от начальных условий не зависят.
Как уже отмечалось ранее, из формулы (21) следует, что изменение каждой из координат 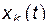 со временем представляет собой наложение
со временем представляет собой наложение  простых гармонических колебаний
простых гармонических колебаний 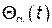 с произвольными амплитудами и фазами, но имеющими вполне определенные частоты
с произвольными амплитудами и фазами, но имеющими вполне определенные частоты 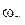 . Но это означает, что всегда от обобщенных координат
. Но это означает, что всегда от обобщенных координат 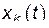 можно перейти к новым обобщенным координатам, чтобы каждая из них соответствовала только одной собственной частоте
можно перейти к новым обобщенным координатам, чтобы каждая из них соответствовала только одной собственной частоте 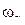 . Ясно, что новыми обобщенными координатами и будут величины
. Ясно, что новыми обобщенными координатами и будут величины 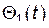 ,
, 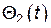 ,…….
,……. 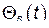 . Это непосредственно следует из самого вида общего решения (21). Действительно, рассматривая
. Это непосредственно следует из самого вида общего решения (21). Действительно, рассматривая  соотношений (21) как систему
соотношений (21) как систему  уравнений относительно неизвестных
уравнений относительно неизвестных 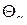 , можно выразить все старые обобщенные координаты
, можно выразить все старые обобщенные координаты  через величины
через величины  ,…….
,…….  :
:
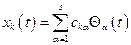 (24)
(24)
Но это как раз и означает, что величины  можно рассматривать как новые обобщенные координаты. Эти координаты называются нормальными координатами (или главными), а совершаемые ими простые гармонические колебания – нормальными колебаниями системы, которым соответствуют нормальные частоты
можно рассматривать как новые обобщенные координаты. Эти координаты называются нормальными координатами (или главными), а совершаемые ими простые гармонические колебания – нормальными колебаниями системы, которым соответствуют нормальные частоты 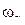 . Поскольку каждая нормальная координата меняется по гармоническому закону
. Поскольку каждая нормальная координата меняется по гармоническому закону 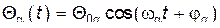 , то каждая из величин
, то каждая из величин 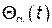 удовлетворяет обычному уравнению для одномерных гармонических колебаний
удовлетворяет обычному уравнению для одномерных гармонических колебаний
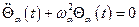 ,
, 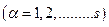 (25)
(25)
Сказанное выше означает, что в нормальных координатах система уравнений (15) распадается на  независимых друг от друга уравнений, с независимыми начальными условиями. Другими словами, нормальные координаты полностью независимы друг от друга. Последнее означает, что функция Лагранжа (15.13), выраженная через нормальные координаты
независимых друг от друга уравнений, с независимыми начальными условиями. Другими словами, нормальные координаты полностью независимы друг от друга. Последнее означает, что функция Лагранжа (15.13), выраженная через нормальные координаты 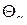 , может быть представлена как сумма функций Лагранжа для каждой нормальной координаты
, может быть представлена как сумма функций Лагранжа для каждой нормальной координаты
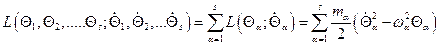 (26)
(26)
Здесь 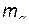 - положительные постоянные.
- положительные постоянные.
Сказанное выше фактически означает, что и потенциальная и кинетическая энергия
 ;
; 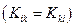
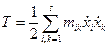 ;
; 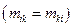 ,
,
могут быть одновременно приведены к диагональному виду.
25Уравнения Гамильтона (канонические уравнения). Функция Гамильтона
Одна из форм уравнения движения, это уравнения Лагранжа, когда задается функция Лагранжа 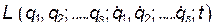 , как функция независимых обобщенных координат и обобщенных скоростей
, как функция независимых обобщенных координат и обобщенных скоростей  , а затем составляется система
, а затем составляется система  уравнений Лагранжа
уравнений Лагранжа
 ,
, 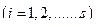 (1)
(1)
Однако такая форма описания механических систем не является единственно возможной. Ряд преимуществ, особенно при исследовании общих теоретических вопросов механики, представляет другая форма записи уравнений движения, когда в качестве независимых переменных выбираются обобщенные координаты и обобщенные импульсы: 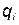 и
и  .
.
Чтобы перейти от набора переменных 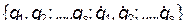 к новому набору переменных
к новому набору переменных 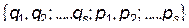 нужно воспользоваться стандартным преобразованием Лежандра. Для этого нужно выразить полный дифференциал функции Лагранжа
нужно воспользоваться стандартным преобразованием Лежандра. Для этого нужно выразить полный дифференциал функции Лагранжа 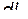 не через дифференциалы
не через дифференциалы 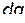 и
и  , а через дифференциалы обобщенных координат и импульсов
, а через дифференциалы обобщенных координат и импульсов 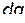 и
и 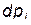 . Тогда величины, стоящие при соответствующих дифференциалах будут частными производными по обобщенным координатам и импульсам от некоторой функции этих же переменных. В результате получим уравнения движения в переменных
. Тогда величины, стоящие при соответствующих дифференциалах будут частными производными по обобщенным координатам и импульсам от некоторой функции этих же переменных. В результате получим уравнения движения в переменных 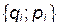 .
.
Рассмотрим сначала для простоты, механическую систему с одной степенью свободы 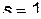 , т.е. с одной обобщенной координатой
, т.е. с одной обобщенной координатой  . Тогда
. Тогда 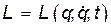 , и уравнение Лагранжа будет имеет вид:
, и уравнение Лагранжа будет имеет вид:
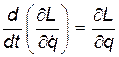 (2)
(2)
В этом случае движение механической системы описывается одним дифференциальным уравнением второго порядка, а независимые переменные 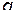 и
и 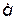 входят в него явно не симметричным образом. Время
входят в него явно не симметричным образом. Время 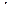 играет в уравнениях Лагранжа роль независимой переменной, т.е. параметра в том смысле, что в эти уравнения не входит производная
играет в уравнениях Лагранжа роль независимой переменной, т.е. параметра в том смысле, что в эти уравнения не входит производная 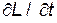 . Уравнение (2) можно формально записать в виде
. Уравнение (2) можно формально записать в виде
 , где
, где 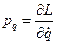 (3)
(3)
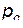 - обобщенный импульс, соответствующий обобщенной координате
- обобщенный импульс, соответствующий обобщенной координате 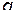 .
.
В рассматриваемом случае преобразование Лежандра сводится к следующему. Вычислим полный дифференциал от функции Лагранжа 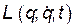 :
:
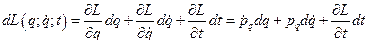 (4)
(4)
В полученном выражении нужно исключить дифференциал 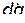 , выразив его через дифференциал
, выразив его через дифференциал 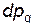 . Для этого воспользуемся очевидным равенством
. Для этого воспользуемся очевидным равенством
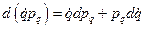

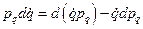 (5)
(5)
Подставляя это в соотношение (4) получим
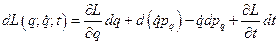 , т.е.
, т.е.
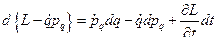 ;
; 
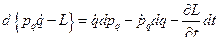 (6)
(6)
Левая часть соотношения (6), есть дифференциал от энергии системы, т.к. по определению
 (7)
(7)
Величина 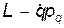 в уравнении (6) выражена через обобщенные координаты и импульсы, т.к. в правой части равенства (6), стоят дифференциалы именно этих величин. Величина
в уравнении (6) выражена через обобщенные координаты и импульсы, т.к. в правой части равенства (6), стоят дифференциалы именно этих величин. Величина
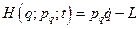 (8)
(8)
называется гамильтоновой функцией системы, или просто функцией Гамильтона. Из дифференциального равенства (6)
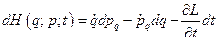 (9)
(9)
или
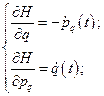 (10)
(10)
Это и есть искомые уравнения в переменных 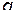 и
и 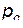 - уравнения Гамильтона.
- уравнения Гамильтона.
Видим, что для системы с одной степенью свободы, уравнения Гамильтона представляют собой два дифференциальных уравнения первого порядка, вместо одного дифференциального уравнения Лагранжа (2) второго порядка. В уравнения (10) переменные 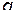 и
и 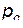 входят симметричным образом. Ввиду их формальной простоты и симметрии эти уравнения называются каноническими уравнениями движения.
входят симметричным образом. Ввиду их формальной простоты и симметрии эти уравнения называются каноническими уравнениями движения.
Наличие слагаемого с 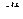 в дифференциальной форме (9), которое учитывает возможную явную зависимость функции Лагранжа (и, как следствие этого, функции Гамильтона) от времени не имеет отношения к выводу самих уравнений Гамильтона, поскольку, как и в уравнениях Лагранжа, время в рассматриваемом аспекте играет роль параметра. Из (9) следует, что
в дифференциальной форме (9), которое учитывает возможную явную зависимость функции Лагранжа (и, как следствие этого, функции Гамильтона) от времени не имеет отношения к выводу самих уравнений Гамильтона, поскольку, как и в уравнениях Лагранжа, время в рассматриваемом аспекте играет роль параметра. Из (9) следует, что
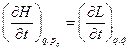 (11)
(11)
Все сказанное выше непосредственно обобщается на систему с любым числом степеней свободы  . В этом случае будем иметь:
. В этом случае будем иметь:
 (12)
(12)
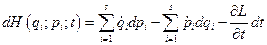 (13)
(13)
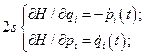 ,
, 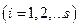 (14)
(14)
Рассмотрим несколько простых примеров.
1. Написать функцию Лагранжа и функцию Гамильтона, а так же уравнения Лагранжа и уравнения Гамильтона в декартовых координатах для частицы  , движущейся в произвольном поле
, движущейся в произвольном поле  .
.
a). Функция и уравнения Лагранжа
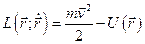 ;
; 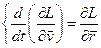 ;
; 
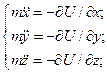 (15)
(15)
b). Функция и уравнения Гамильтона. Т.к. 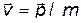 , то
, то
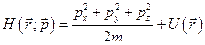 ;
; 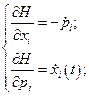 , т.е.
, т.е.
 (16)
(16)
Видим, что и те и другие уравнения фактически сводятся ко второму закону Ньютона.
2. Написать функцию Лагранжа и функцию Гамильтона, а так же уравнения Лагранжа и уравнения Гамильтона в цилиндрических координатах для частицы  , движущейся в произвольном поле
, движущейся в произвольном поле  .
.
a). Функция и уравнения Лагранжа
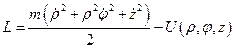 ;
; 
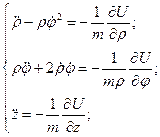 (17)
(17)
b). Функция и уравнения Гамильтона
Сначала нужно записать функцию Гамильтона, т.е. выразить энергию системы
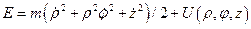 через обобщенные импульсы
через обобщенные импульсы
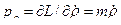 ;
; 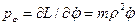 ;
; 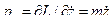 (18)
(18)
Отсюда выражаем обобщенные скорости через обобщенные импульсы:
 ;
; 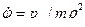 ;
;  (19)
(19)
Подставляя это в формулу для энергии, получим выражение для функции Гамильтона:
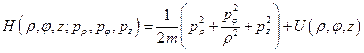 (20)
(20)
Уравнения Гамильтона в цилиндрических координатах
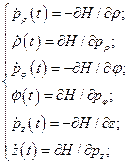

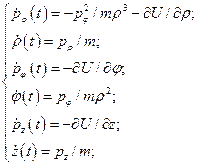 (21)
(21)
3. Записать уравнения Гамильтона для линейного гармонического осциллятора, когда 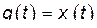 и
и  .
.
 ;
; 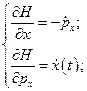

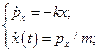 (22)
(22)
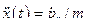 ;
; 
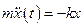 ;
; 
 (23)
(23)
Получили обычное уравнение для линейного осциллятора.
4. Записать уравнения Гамильтона для математического маятника 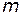 длиной
длиной 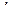 , который совершает колебания в вертикальной плоскости. Ось
, который совершает колебания в вертикальной плоскости. Ось 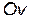 направлена вниз, так, что
направлена вниз, так, что 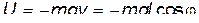 .
. 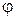 - угол отклонения от положения равновесия.
- угол отклонения от положения равновесия.
В цилиндрических координатах
 ;
; 
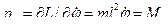 ;
;
 ;
; 
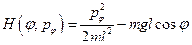 (24)
(24)
Уравнения Гамильтона
 ,
, 
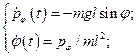 (25)
(25)
т.е.
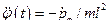 ;
; 
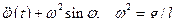 (26)
(26)
Получили обычное уравнение колебания математического маятника.
Введем теперь понятие скобок Пуассона. Пусть имеется механическая система с одной степенью свободы: 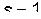 . Её обобщенные координата
. Её обобщенные координата 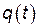 и импульс
и импульс 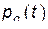 удовлетворяют уравнениям Гамильтона (10)
удовлетворяют уравнениям Гамильтона (10)
 (27)
(27)
Пусть 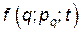 - некоторая функция величин
- некоторая функция величин 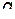 ,
,  и времени
и времени  . Составим её полную производную по времени, учитывая, что величины
. Составим её полную производную по времени, учитывая, что величины 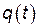 и
и 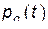 тоже зависят от времени
тоже зависят от времени
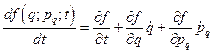 (28)
(28)
Поскольку 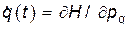 и
и 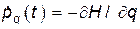 , то выражение (28) принимает вид
, то выражение (28) принимает вид
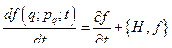 (29)
(29)
Здесь введено обозначение
 (30)
(30)
Выражение 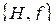 , определяемое формулой (30) называется скобкой Пуассона для величин
, определяемое формулой (30) называется скобкой Пуассона для величин 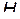 и
и  . Если число степеней свободы механической системы больше единицы, то скобка Пуассона функции Гамильтона и некоторой функции динамических переменных
. Если число степеней свободы механической системы больше единицы, то скобка Пуассона функции Гамильтона и некоторой функции динамических переменных 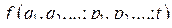 равна
равна
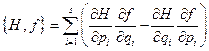 (31)
(31)
где  - число степеней свободы системы. Для любой пары функций динамических переменных скобка Пуассона определяется аналогично формуле (31)
- число степеней свободы системы. Для любой пары функций динамических переменных скобка Пуассона определяется аналогично формуле (31)
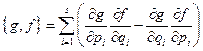 (32)
(32)
 2020-08-05
2020-08-05 233
233








