29 Канонические преобразования. Производящие функции. Временная эволюция механической системы как каноническое преобразование
Выбор обобщенных координат 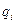 не ограничен никакими условиями – ими могут быть любые величин, однозначно определяющие положение системы в пространстве. Формальный вид уравнений Лагранжа от этого выбора не зависит, поэтому можно сказать, что уравнения Лагранжа инвариантны по отношению к преобразованию координат
не ограничен никакими условиями – ими могут быть любые величин, однозначно определяющие положение системы в пространстве. Формальный вид уравнений Лагранжа от этого выбора не зависит, поэтому можно сказать, что уравнения Лагранжа инвариантны по отношению к преобразованию координат 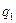 ,
, 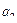 , …,
, …,  к любым другим независимым величинам
к любым другим независимым величинам 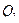 ,
, 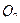 , …,
, …, 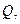 . Новые координаты являются функциями старых, причем допустим и такой их выбор, который содержит явным образом время
. Новые координаты являются функциями старых, причем допустим и такой их выбор, который содержит явным образом время
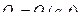 (1)
(1)
Наряду с уравнениями Лагранжа сохраняют свой вид и уравнения Гамильтона. Последние, однако, допускают гораздо более широкий класс преобразований. Это связано с тем, что в гамильтоновом методе импульсы 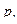 играют наряду с координатами
играют наряду с координатами 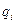 роль равноправных независимых переменных. Поэтому понятие преобразования может быть расширено так, чтобы включить в себя преобразование всех
роль равноправных независимых переменных. Поэтому понятие преобразования может быть расширено так, чтобы включить в себя преобразование всех 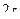 независимых переменных
независимых переменных 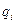 и
и 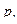 к новым переменным
к новым переменным 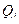 и
и 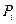 по формулам
по формулам
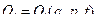
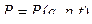 (2)
(2)
Такое расширение класса допустимых преобразований является одним из существенных достоинств гамильтонова метода.
Однако не при произвольных преобразованиях вида (2) уравнения движения сохраняют свой канонический вид. Выведем условия, которым должно удовлетворять преобразование, для того чтобы уравнения движения в новых переменных 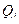 и
и 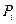 имели вид
имели вид
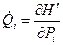
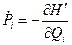 (3)
(3)
с некоторой новой функцией Гамильтона 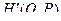 . Такие преобразования координат и импульсов называют каноническими.
. Такие преобразования координат и импульсов называют каноническими.
К формулам канонических преобразований можно придти из следующих соображений. Уравнения Гамильтона можно вывести из принципа наименьшего действия, представленного в форме
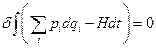 (4)
(4)
(причем варьируются независимо все координаты и импульсы). Для того чтобы новые переменные 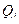 и
и 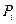 тоже удовлетворяли уравнениям Гамильтона, для них тоже должен быть справедлив принцип наименьшего действия
тоже удовлетворяли уравнениям Гамильтона, для них тоже должен быть справедлив принцип наименьшего действия
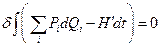 (5)
(5)
Два принципа (4) и (5) эквивалентны друг другу только при условии, что их подынтегральные выражения отличаются лишь на полный дифференциал произвольной функции 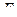 координат, импульсов и времени; тогда разность между обоими интегралами будет несущественной при варьировании постоянной (разность значений
координат, импульсов и времени; тогда разность между обоими интегралами будет несущественной при варьировании постоянной (разность значений 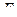 на пределах интегрирования). Таким образом, должно быть:
на пределах интегрирования). Таким образом, должно быть:
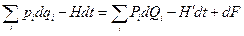
Всякое каноническое преобразование характеризуется своей функцией 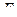 , которую называют производящей функцией данного преобразования. Переписав полученное соотношение в виде
, которую называют производящей функцией данного преобразования. Переписав полученное соотношение в виде
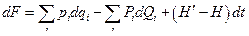 (6)
(6)
мы видим, что
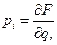
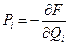
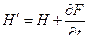 (7)
(7)
при этом предполагается, что производящая функция задана как функция старых и новых координат (и времени): 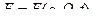 . При заданной функции
. При заданной функции 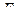 формулы (7) устанавливают связь между старыми
формулы (7) устанавливают связь между старыми  и новыми
и новыми 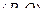 переменными, а также дают выражение для новой гамильтоновой функции.
переменными, а также дают выражение для новой гамильтоновой функции.
Может оказаться удобным выражать производящую функцию не через переменные  и
и 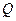 , а через старые координаты
, а через старые координаты  и новые импульсы
и новые импульсы 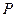 . Для вывода формул канонических преобразований в этом случае надо произвести в соотношении (6) соответствующее преобразование Лежандра. Именно, переписываем его в виде
. Для вывода формул канонических преобразований в этом случае надо произвести в соотношении (6) соответствующее преобразование Лежандра. Именно, переписываем его в виде
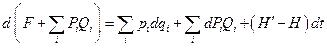
Выражение, стоящее под знаком дифференциала в левой стороне равенства, выраженное через переменные  и
и 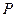 , является новой производящей функцией. Обозначив ее посредством
, является новой производящей функцией. Обозначив ее посредством 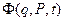 имеем:
имеем:
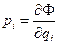
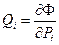
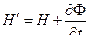 (8)
(8)
Аналогичным образом можно перейти к формулам канонических преобразований, выраженных через производящие функции, зависящие от переменных 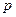 и
и 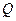 или
или 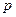 и
и 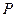 .
.
Отметим, что связь между новой и старой гамильтоновыми функциями всегда выражается одинаковым образом: разность  дается частной производной по времени от производящей функции. В частности, если последняя не зависит от времени, то
дается частной производной по времени от производящей функции. В частности, если последняя не зависит от времени, то 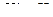 . Другими словами, в этом случае для получения новой функции Гамильтона достаточно подставить в
. Другими словами, в этом случае для получения новой функции Гамильтона достаточно подставить в 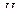 величины
величины  и
и 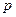 , выраженные через новые переменные
, выраженные через новые переменные 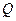 и
и 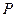 .
.
Широта канонических преобразований в значительной степени лишает в гамильтоновом методе понятие обобщенных координат и импульсов их первоначального смысла. Поскольку преобразования (2) связывают каждую из величин 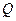 и
и 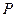 как с координатами
как с координатами  , так и с импульсами
, так и с импульсами 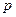 , то переменные
, то переменные 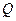 уже не имеют смысла чисто пространственных координат. Различие между обеими группами переменных становится в основном вопросом номенклатурным. Это обстоятельство весьма наглядно проявляется, например, в преобразовании
уже не имеют смысла чисто пространственных координат. Различие между обеими группами переменных становится в основном вопросом номенклатурным. Это обстоятельство весьма наглядно проявляется, например, в преобразовании 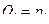 ,
, 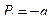 , явно не меняющем канонический вид уравнений и сводящемся просто ко взаимному переименованию координат и импульсов.
, явно не меняющем канонический вид уравнений и сводящемся просто ко взаимному переименованию координат и импульсов.
В виду этой условности терминологии переменные 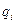 и
и 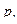 в гамильтоновом методе часто называют просто канонически сопряженными величинами.
в гамильтоновом методе часто называют просто канонически сопряженными величинами.
 2020-08-05
2020-08-05 149
149








