Экспериментальное определение МХ ИК ИИС (по протоколу измерений)

Измерение метрологических характеристик ИК ИИС состоит в проведении многократного измерения выходного сигнала в разных точках диапазона в условиях, максимально приближенных к реальным рабочим условиям эксплуатации ИИС.

На вход ИК подают последовательность значений сигнала в пяти контрольных точках шкалы от минимального значения до максимального и регистрируют значения выходных сигналов. В протоколах измерений, выдаваемых преподавателем каждому студенту, приведены данные 6-ти значений результата многократного измерения и допустимое отклонение функции преобразования D_доп ИК от номинального значения функции преобразования в каждой из точек.

Вычисляются: S – мера неопределенности показаний ИК; u_θ – мера неопределенности поправки к показаниям ИК; u -мера неопределенности измеряемой величины.

Результаты измерений и расчетов следует занести в табл.4.

Таблица 4

Данные в контрольных точках			Результаты измерений в контрольных точках у_ij						Результаты расчетов
j	x_j	D_доп	1	2	3	4	5	6		S_j	u_θj	u_j
1
2
3
4
5

Порядок расчета:

1) В каждой контрольной точке шкалы определяются средние арифметические значения результата измерений по формуле:

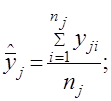(26)

где y_ji – результат измерения в j - ой контрольной точке, n_j – число отсчетов в j - ой контрольной точке.

2) В каждой контрольной точке вычисляется стандартное отклонение (мера неопределенности, оцениваемая по типу А):

(27)

3) В каждой контрольной точке вычисляется мера неопределенности поправки к показаниям ИК, вычисляемая по типу В. При этом в качестве математической модели неопределенной ситуации принимается равномерный закон распределения вероятности:

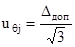(28)

4) В каждой контрольной точке вычисляется мера неопределенности измеряемой величины.

(29)

Принимаем коэффициент охвата k=2.

5) По результатам расчетов строятся дискретные значения функция преобразования с учетом полученных значений u_j. Мера неопределенности входного параметра считается пренебрежимо малой.

ЗАДАНИЕ 4