Скалярное произведение двух векторов 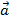 и
и 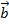 – число равное
– число равное 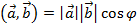 , где
, где 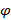 – угол между векторами
– угол между векторами 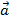 и
и 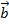 .
.
Свойства скалярного произведения
1. 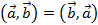
2. 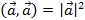
3. 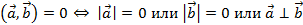
4. 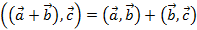
5. 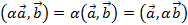
Теорема 1: Если 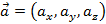 и
и 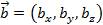 , тогда
, тогда 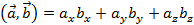 .
.
Следствие 1: 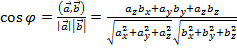 .
.
Векторное произведение векторов
Векторным произведением двух векторов 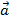 и
и 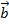 называется такой вектор
называется такой вектор 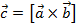 , для которого выполняются условия:
, для которого выполняются условия:
1. 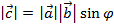 , где
, где 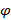 – угол между векторами
– угол между векторами 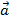 и
и 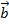 ;
;
2. 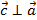 и
и 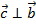 ;
;
3. Направление 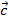 задается по правилу правой руки.
задается по правилу правой руки.
Свойства векторного произведения
1. 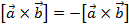
2. 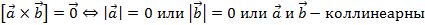
3. 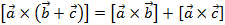
4. 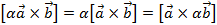
Теорема 1: Если 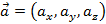 и
и 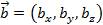 , тогда векторное произведение определяется соотношением
, тогда векторное произведение определяется соотношением
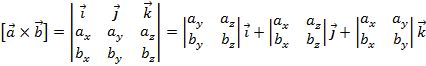
Геометрический смысл векторного произведения – определение площади параллелограмма S, из которого можно найти площадь треугольника 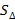
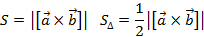
Следствие 1: 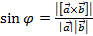 .
.
Направляющие косинусы
Пусть 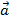 образует с координатными осями Ox, Oy, Oz углы
образует с координатными осями Ox, Oy, Oz углы 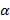 ,
, 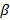 и
и 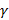 соответственно, тогда
соответственно, тогда  ,
, 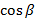 и
и 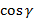 называют направляющими косинусами
называют направляющими косинусами 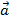
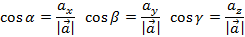
Вектор с координатами из направляющих косинусов – отнормированный вектор 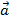
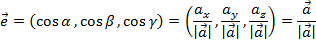
Смешанное произведение векторов
Смешанным произведением трех векторов 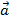 ,
, 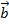 и
и 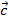 называется число
называется число
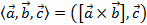
Теорема 1: Если 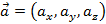 ,
, 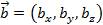 и
и 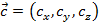 , тогда смешанное произведение векторов определяется как
, тогда смешанное произведение векторов определяется как
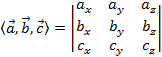
Геометрический смысл смешанного произведения – определение объема параллелепипеда V и пирамиды 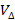
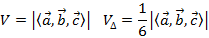
Свойства смешанного произведения
1. 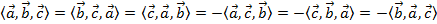
2. 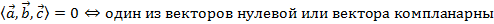
3. 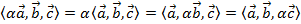
Признаки расположения векторов
Пусть 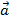 ,
, 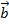 и
и 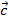 не нулевые векторы, тогда
не нулевые векторы, тогда
1. 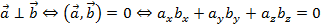
2. 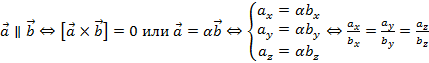
3. 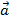 ,
, 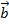 и
и 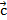 – компланарны
– компланарны 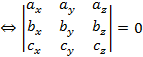
Правила проверки на линейную зависимость векторов
Два вектора линейно зависимы, если присутствует пропорциональность их координат: 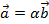 .
.
Три вектора линейно зависимы, если они компланарны: 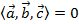 .
.
Четыре и более векторов в трехмерном пространстве 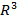 всегда линейно зависимы.
всегда линейно зависимы.
Аналитическая геометрия
Прямая на плоскости
Уравнение с угловым коэффициентом 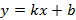 задает все не вертикальные прямые (рисунок 5). В данном уравнении коэффициент
задает все не вертикальные прямые (рисунок 5). В данном уравнении коэффициент 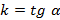 , который влияет на прямую следующим образом:
, который влияет на прямую следующим образом: 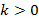 – прямая возрастает,
– прямая возрастает, 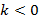 – прямая убывает,
– прямая убывает, 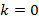 – прямая параллельная оси Ox.
– прямая параллельная оси Ox.
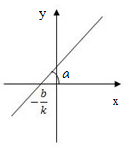
Рисунок 5. Прямая, заданная уравнением с угловым коэффициентом.
Вертикальная прямая имеет уравнение 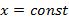 и его невозможно получить из рассматриваемого уравнения.
и его невозможно получить из рассматриваемого уравнения.
Прямая, проходящая через точку 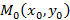 и вектор нормали
и вектор нормали 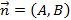 имеет уравнение
имеет уравнение 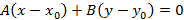 . Построение такого вида прямой представлено на рисунке 6.
. Построение такого вида прямой представлено на рисунке 6.
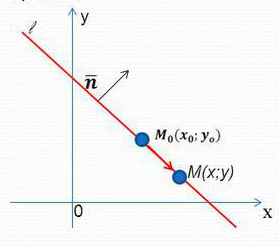
Рисунок 6. Прямая, проходящая через заданную точку и вектор нормали.
Для построения такого вида прямых задается дополнительная точка
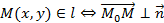 и исходя из координат вектора
и исходя из координат вектора 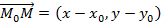 выводится указанное уравнение.
выводится указанное уравнение.
Преобразовав уравнение прямой, проходящей через точку и вектор нормали, можно получить общее уравнение прямой вида 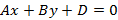 , где A и B – координаты вектора нормали. Полученное уравнение задает все прямые, в том числе и вертикальные прямые.
, где A и B – координаты вектора нормали. Полученное уравнение задает все прямые, в том числе и вертикальные прямые.
Преобразовав уже общее уравнение прямой, будет получено уравнение в прямой в отрезках вида
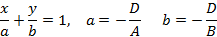
Построение прямой такого вида представлено на рисунке 7.
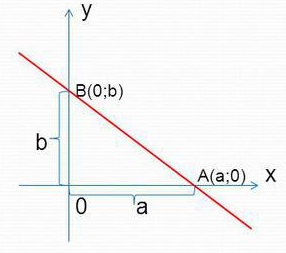
Рисунок 7. Построение прямой, заданном в уравнении в отрезках.
Дальнейший анализ возможности задать прямую на плоскости приведет еще к двум видам уравнений. Первым из них является параметрическое уравнение прямой, проходящей через точку 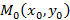 и направляющий вектор
и направляющий вектор 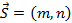
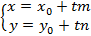
Из полученного уравнения вытекает каноническое уравнение прямой
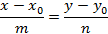
Построение прямой по последним двум последним уравнениям представлены на рисунке 8.
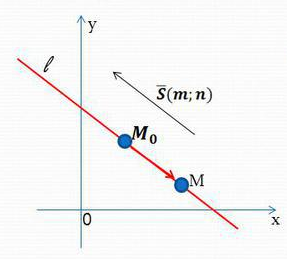
Рисунок 8. Построение прямой, заданной точкой и направляющим вектором.
Помимо всех вышеуказанных способов существует еще способ задания прямой с помощью двух точек 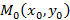 и
и 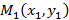
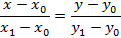
Пример прямой такого вида представлен на рисунке 9.
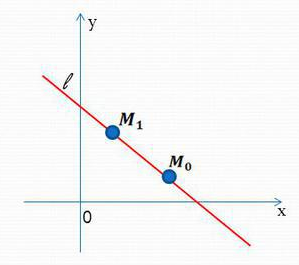
Рисунок 9. Прямая, заданная с помощью двух точек.
Помимо способов задания прямой на плоскости, следует определить признаки взаимного расположения прямых на плоскости. Если прямые заданы уравнением с угловым коэффициентом, тогда тангенс угла между заданными прямыми 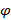 , имеющими уравнения
, имеющими уравнения 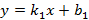 и
и 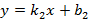 будет равен
будет равен
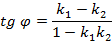
Исходя из этого уравнения, выделены признаки взаимного расположения прямых: при
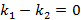 – прямые параллельны и при
– прямые параллельны и при 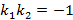 – прямые перпендикулярны.
– прямые перпендикулярны.
Рассматривая общие уравнения прямых, которые имеют вид 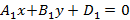 и
и
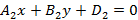 получим косинус угла между прямыми
получим косинус угла между прямыми 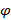 равным
равным
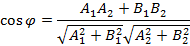
Аналогично предыдущему случаю, из этого уравнения вытекают признаки параллельности прямых, если 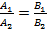 и признак перпендикулярности, если
и признак перпендикулярности, если 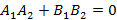 . Угол
. Угол 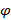 также является углом между нормалями указанных прямых.
также является углом между нормалями указанных прямых.
Используя общее уравнение прямой 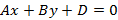 , можно найти расстояние d от любой точки
, можно найти расстояние d от любой точки 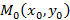 до этой прямой
до этой прямой
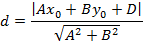
Расстоянием считается минимальный отрезок (перпендикуляр) от заданной точки до указанной прямой.
 2020-08-05
2020-08-05 136
136








