Поскольку пересечение двух плоскостей в пространстве задают прямую, тогда данная прямая в пространстве описывается системой общих уравнений пересекающихся плоскостей
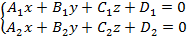
Построение прямой, указанным способом представлено на рисунке 13.
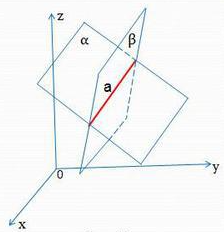
Рисунок 13. Прямая, заданная пересечением двух плоскостей.
Вторым способом задания прямой в пространстве является задание прямой с помощью точки 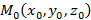 лежащей на прямой и направляющего вектора
лежащей на прямой и направляющего вектора 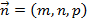 . Из этих данных можно получить параметрическое уравнение прямой в пространстве
. Из этих данных можно получить параметрическое уравнение прямой в пространстве
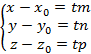
Построение прямой с помощью точки и направляющего вектора представлено на рисунке 14.
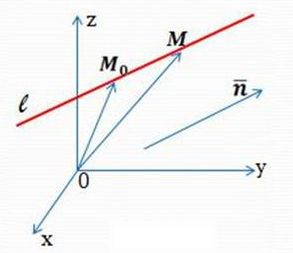
Рисунок 14. Задание прямой с помощью точки и направляющего вектора.
Преобразовав данное уравнение, получим каноническое уравнение прямой в пространстве
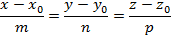
Последний рассматриваемый способ построения прямой в пространстве подразумевает введение второй точки 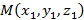 , следовательно возможно получить уравнение прямой в пространстве, проходящей через две заданные точки
, следовательно возможно получить уравнение прямой в пространстве, проходящей через две заданные точки
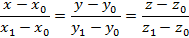
Проанализируем признаки взаимного расположения прямых в пространстве. Пусть заданы две прямые 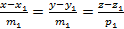 и
и 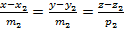 , тогда заданные прямые пересекаются или скрещиваются под углом
, тогда заданные прямые пересекаются или скрещиваются под углом 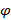 равным
равным
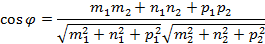
Исходя из этого уравнения, прямые параллельны, если 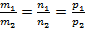 или прямые перпендикулярны, если
или прямые перпендикулярны, если 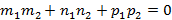 .
.
Кривые второго порядка
Кривой второго порядка называется линия, которая задается уравнением второго порядка вида
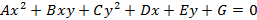
В данном уравнении A, B и C – не равны нулю одновременно.
С помощью рассматриваемого уравнения могут быть заданы кривые следующих типов (случаи 4 – 7 называются вырожденными):
1. Эллипс;
2. Гипербола;
3. Парабола;
4. Мнимый эллипс 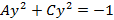 ;
;
5. Пара пересекающихся прямых 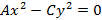 ;
;
6. Пара параллельных прямых 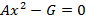 ;
;
7. Точка 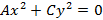 .
.
Эллипс
Пусть даны две точки 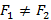 , которые называются фокусами. Множество всех точек
, которые называются фокусами. Множество всех точек  таких, что
таких, что  – сумма расстояний от
– сумма расстояний от  до фокусов постоянно называется эллипсом. Пример эллипса представлен на рисунке 15.
до фокусов постоянно называется эллипсом. Пример эллипса представлен на рисунке 15.
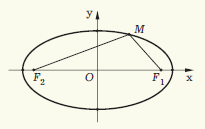
Рисунок 15. Изображение эллипса.
Рассмотрим эллипс на координатной плоскости так чтобы его фокусы были симметричны относительно Oy и лежали на оси Ox (рисунок 16).
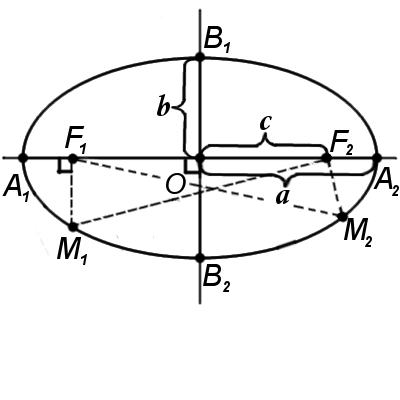
Рисунок 16. Расположение эллипса на координатной плоскости.
Пусть 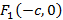 и
и 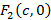 , таким образом межфокусное расстояние
, таким образом межфокусное расстояние 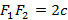 . Обозначим расстояние из определения
. Обозначим расстояние из определения 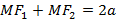 , в котором
, в котором
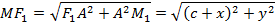
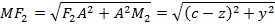
Таким образом получим соотношение
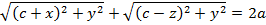
Преобразовав полученное соотношение, получим простейшее уравнение эллипса
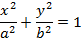
В полученном уравнении a и b – большие и малые полуоси соответственно. При 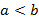 – эллипс втянут по вертикали, а его фокусы будут лежат на оси Oy. Если
– эллипс втянут по вертикали, а его фокусы будут лежат на оси Oy. Если 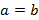 , тогда эллипс превратится в окружность, при этом межфокусное расстояние будет равно нулю и будут лежать в начале координат. Уравнение окружности в данном случае примет вид
, тогда эллипс превратится в окружность, при этом межфокусное расстояние будет равно нулю и будут лежать в начале координат. Уравнение окружности в данном случае примет вид
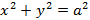
Если центр эллипса находится в произвольной точке 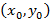 , тогда уравнение эллипса со смещенным центром примет вид
, тогда уравнение эллипса со смещенным центром примет вид
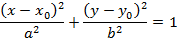
Уравнение окружности со смещенным центром, в таком случае, примет вид
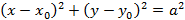
Гипербола
Зафиксируем две точки 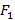 и
и 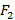 , которые называют фокусами, тогда множество точек M таких, что модуль разности от заданной точки до фокусов
, которые называют фокусами, тогда множество точек M таких, что модуль разности от заданной точки до фокусов 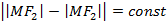 называется гиперболой.
называется гиперболой.
Обозначим 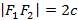 и расположим фокусы
и расположим фокусы 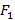 и
и 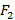 на оси Ox симметрично, относительно начала координат. Пусть некоторая константа
на оси Ox симметрично, относительно начала координат. Пусть некоторая константа 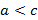 и рассмотрим точки
и рассмотрим точки 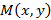 , такие что
, такие что 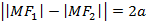 , тогда будут получены соотношения
, тогда будут получены соотношения
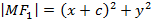
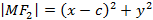
Исходя из этого, получим соотношение
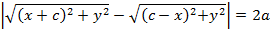
Из полученного соотношения получим простейшее уравнение гиперболы
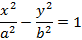
Пример гиперболы представлен на рисунке 17.
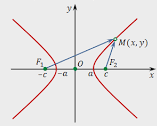
Рисунок 17. Изображение гиперболы.
Исследовав полученное уравнение гиперболы, получим асимптотические прямые вида 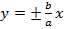 , к которым стремятся ветви гиперболы. Построение гиперболы относительно асимптотических прямых представлено на рисунке 18.
, к которым стремятся ветви гиперболы. Построение гиперболы относительно асимптотических прямых представлено на рисунке 18.
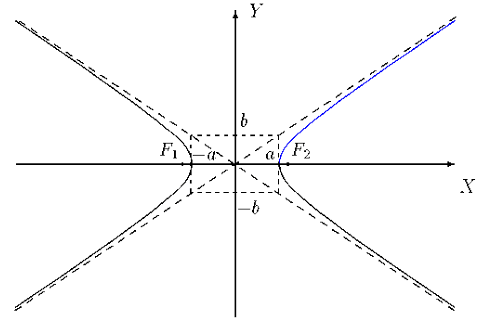
Рисунок 18. Гипербола относительно асимптотических прямых.
Прямоугольник с вершинами 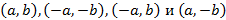 называется характеристическим. Его диагонали задают направление асимптотических прямых.
называется характеристическим. Его диагонали задают направление асимптотических прямых.
Если фокусы гиперболы расположить симметрично относительно Oy, тогда ее уравнение примет вид
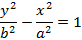
Если центр гиперболы сместить в точку 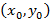 , тогда уравнение гиперболы примет вид
, тогда уравнение гиперболы примет вид
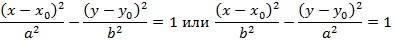
Парабола
Зафиксируем точку 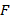 – фокус и прямую
– фокус и прямую 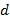 – директриса, такая что
– директриса, такая что 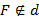 . Множество всех точек M, равноудаленных от фокуса и директрисы
. Множество всех точек M, равноудаленных от фокуса и директрисы 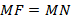 называется параболой. Обозначим p – расстояние от фокуса до директрисы и расположим
называется параболой. Обозначим p – расстояние от фокуса до директрисы и расположим 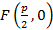 на си Ox, а директрису перпендикулярную Ox. Построение подставлено на рисунке 19.
на си Ox, а директрису перпендикулярную Ox. Построение подставлено на рисунке 19.
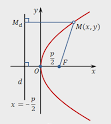
Рисунок 19. Изображение параболы.
При таких условиях парабола пройдет через начало координат. Уравнение такого вида параболы имеет вид
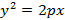
Если 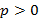 , тогда ветви параболы направлены в сторону увеличения x; при
, тогда ветви параболы направлены в сторону увеличения x; при 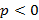 , тогда ветви параболы направлены в сторону уменьшения x. Если в рассматриваемом уравнении поменять роли x и y таким образом, что
, тогда ветви параболы направлены в сторону уменьшения x. Если в рассматриваемом уравнении поменять роли x и y таким образом, что 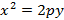 , тогда ветви параболы будут смотреть в сторону увеличения y (
, тогда ветви параболы будут смотреть в сторону увеличения y (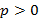 ) или в сторону уменьшения y (
) или в сторону уменьшения y (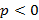 ).
).
Если вершину параболы сместить в точку 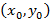 , тогда уравнения примут вид
, тогда уравнения примут вид
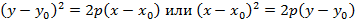
Пример параболы со смещенным центром представлен на рисунке 20.
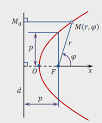
Рисунок 20. Изображение параболы со смещенным центром.
 2020-08-05
2020-08-05 170
170








