Линейной комбинацией векторов  называется выражение вида
называется выражение вида
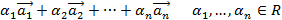
Если хотя бы один из коэффициентов равен нулю, тогда линейная комбинация векторов называется нетривиальной.
Тривиальная линейная комбинация всегда равна нулевому вектору. Если линейная комбинация не нулевых векторов равен 0, это не означает, что данная линейная комбинация тривиальна. Пример такой комбинации вида 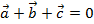 представлен на рисунке 4.
представлен на рисунке 4.

Рисунок 4. Нетривиальная нулевая линейная комбинация.
Набор векторов  называется линейно зависимым, если хотя бы один из них можно представить как линейную комбинацию остальных. Рассматриваемый набор векторов называется линейно независимыми, если ни один из них нельзя представить как линейную комбинацию остальных.
называется линейно зависимым, если хотя бы один из них можно представить как линейную комбинацию остальных. Рассматриваемый набор векторов называется линейно независимыми, если ни один из них нельзя представить как линейную комбинацию остальных.
Набор векторов  называется линейно зависимым, если существует нетривиальная линейная комбинация этих векторов равная нулевому вектору.
называется линейно зависимым, если существует нетривиальная линейная комбинация этих векторов равная нулевому вектору.

Если линейная комбинация рассматриваемых векторов, равная нулевому вектору, является тривиальной, тогда вектора являются линейно независимыми.
Рассмотрим эти понятия для векторов, лежащих на прямой, на плоскости и в пространстве.
Теорема 1: Любые два вектора, лежащие на одной прямой всегда линейно зависимы.
Следствие 1: Максимальное число линейно независимых векторов на прямой равно одному.
Теорема 2: Если два вектора на плоскости неколлинеарные, тогда они линейно независимые.
Теорема 3: Любые три вектора на плоскости всегда линейно зависимые.
Следствие 2: Максимальное число линейно независимых векторов на плоскости равно двум.
Теорема 4: Три некомпланарных вектора в пространстве линейно независимые.
Теорема 5: Четыре вектора в пространстве всегда линейно зависимые.
Следствие 3: Максимальное число линейно независимых векторов в пространстве равно трем.
Базисом в векторном пространстве называется набор векторов 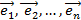 со следующими свойствами: линейная независимость и любой вектор пространства можно выразить через базисные вектора.
со следующими свойствами: линейная независимость и любой вектор пространства можно выразить через базисные вектора.
Базисом на прямой называется любой ненулевой вектор 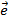 . Любой вектор на прямой можно выразить через соотношение
. Любой вектор на прямой можно выразить через соотношение
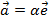
Базисом на плоскости называется набор из двух любых неколлинеарных векторов 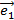 и
и 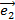 . Любой вектор на плоскости можно выразить через базисные вектора следующим соотношением
. Любой вектор на плоскости можно выразить через базисные вектора следующим соотношением

Базисом в пространстве называется набор из трех любых некомпланарных векторов 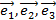 . Любой вектор в пространстве выражается через базисные вектора следующим выражением
. Любой вектор в пространстве выражается через базисные вектора следующим выражением
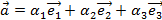
Координатами вектора 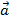 относительно базиса
относительно базиса 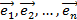 называются коэффициенты
называются коэффициенты  из линейной комбинации векторов. Ортами называются вектора единичной длинны, сонаправленные с осями координат. Координаты вектора – координаты его концевой точки, если начало вектора совпадает с началом координат.
из линейной комбинации векторов. Ортами называются вектора единичной длинны, сонаправленные с осями координат. Координаты вектора – координаты его концевой точки, если начало вектора совпадает с началом координат.
В любом базисе при сложении векторов их координаты складываются, а при умножении вектора на число, каждая координата умножается на это число. В базисе из ортов длина вектора 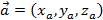 равна
равна

Если 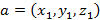 и
и 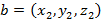 , тогда
, тогда  .
.
Отнормировать вектор означает построить или найти сонаправленный вектор единичной длины.
a 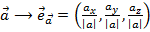
 2020-08-05
2020-08-05 258
258








