Пусть задана точка 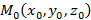 и вектор нормали
и вектор нормали 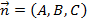 . С их помощью можно найти уравнение плоскости, проходящей через заданную точку и вектор нормали. Данное уравнение имеет вид
. С их помощью можно найти уравнение плоскости, проходящей через заданную точку и вектор нормали. Данное уравнение имеет вид
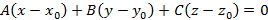
Построение такого вида плоскости представлено на рисунке 10. Для построения выбирается произвольная точка 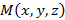 , тогда полученный вектор
, тогда полученный вектор
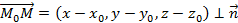 , из которого выводится рассматриваемое уравнение.
, из которого выводится рассматриваемое уравнение.

Рисунок 10. Плоскость, заданная с помощью точки и вектора нормали.
Преобразовав предыдущее уравнение можно получить общее уравнение плоскости
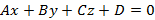
Если 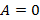 , тогда уравнение плоскости примет вид
, тогда уравнение плоскости примет вид 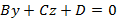 и задает плоскость параллельную Ox. Аналогично, если
и задает плоскость параллельную Ox. Аналогично, если  , тогда уравнение плоскости примет вид
, тогда уравнение плоскости примет вид 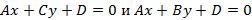 соответственно и задают плоскости параллельные Oy и Oz соответственно. Если
соответственно и задают плоскости параллельные Oy и Oz соответственно. Если 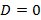 , тогда получим уравнение
, тогда получим уравнение  , которая задает плоскость, проходящую через начало координат.
, которая задает плоскость, проходящую через начало координат.
Дальнейшее преобразования общего уравнения плоскости при условии
 , тогда получим уравнение плоскости в отрезках
, тогда получим уравнение плоскости в отрезках
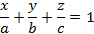
В данном уравнении a, b и c – точки пересечения с соответствующими осями координат и не равны нулю. Построение плоскости такого вида представлено на рисунке 11.
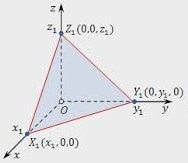
Рисунок 11. Плоскость, заданная с помощью уравнения в отрезках.
Помимо вышеуказанных способов задания плоскости в пространстве, также плоскость можно задать с помощью трех точек в пространстве 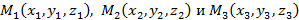 , которые не лежат на одной прямой. Способ построения плоскости такого вида представлен на рисунке 12.
, которые не лежат на одной прямой. Способ построения плоскости такого вида представлен на рисунке 12.
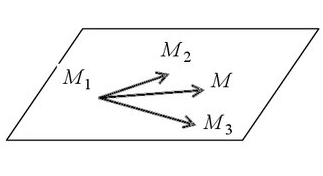
Рисунок 12. Плоскость, заданная с помощью трех точек.
Способ построения подразумевает введения четвертой точки 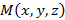 , которая лежит в плоскости, также, как и заданные точки, что позволяет задать три компланарных вектора. Исходя из этого уравнение плоскости, заданной с помощью трех точек, имеет вид
, которая лежит в плоскости, также, как и заданные точки, что позволяет задать три компланарных вектора. Исходя из этого уравнение плоскости, заданной с помощью трех точек, имеет вид
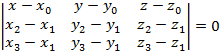
Помимо рассмотренных способов задания плоскости в пространстве, важным также является анализ взаимного расположения плоскостей в пространстве. Пусть заданы две плоскости в пространстве  и
и 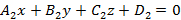 . Если угол между плоскостями равен
. Если угол между плоскостями равен 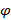 , тогда угол между плоскостями также равен
, тогда угол между плоскостями также равен 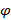 . Исходя из этого угол
. Исходя из этого угол 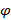 вычисляется на основе координат векторов нормалей заданных плоскостей
вычисляется на основе координат векторов нормалей заданных плоскостей
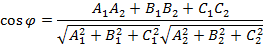
Исходя из данного уравнения признаки расположения плоскостей в пространстве будут иметь вид: 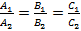 – плоскости параллельны или
– плоскости параллельны или  – плоскости перпендикулярны.
– плоскости перпендикулярны.
Если задана плоскость 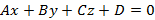 и точка
и точка 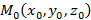 не лежащая на плоскости, тогда расстояние d от этой точки до плоскости равно
не лежащая на плоскости, тогда расстояние d от этой точки до плоскости равно
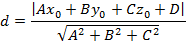
 2020-08-05
2020-08-05 148
148








