Множества и действия с ними

       Множество относится к неопределяемым понятиям. Множество задается своими элементами одной или различной природы. Множество при его описании задается перечислением его элементов в фигурных скобках. В других случаях, в фигурных скобках задается правило составления элементов или их общие признаки

       Множество, не имеющие элементов, называют пустым множеством . Например, множество действительных решений для уравнения  является пустым, хотя имеются два комплексных корня.

       Над множествами можно проводить следующие действия:

1. Сравнение

Если все элементы множества A принадлежат множеству B, тогда A – подмножество B

Если при этом , тогда  – A совпадает с B кроме некоторых элементов.

 – A и B состоит из одинаковых элементов. Порядок следования элементов в обычном множестве не важен. В случае повторения элементов, учитывается каждый из них единожды с учетом его кратности.

2. Объединение – множество , состоящее из всех элементов этих множеств.

3. Пересечение – множество , состоящее из общих элементов для этих множеств.

4. Дополнение – множество , состоящее из элементов универсального множества 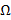, которые не принадлежат множеству A.

5. Разность – множество , состоящее из элементов множества A, которые не принадлежат B.

Указанные операции над множествами обладают следующими свойствами:

1.  – любое равенство можно прочесть и справа на лево, и слева на право;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. .