Множество называют конечным, если оно имеет конечное число различных элементов; такое число называют мощностью множества и обозначают 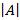 . Комбинаторика – раздел математики, изучающий количества возможных комбинаций.
. Комбинаторика – раздел математики, изучающий количества возможных комбинаций.
Прямым или Декартовым произведением множеств A и B является множество следующего вида 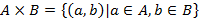 , иными словами, множество всевозможных пар элементов, где первым берется элемент из первого множества, а вторым – из второго множества. Аналогично задается произведение из нескольких множеств.
, иными словами, множество всевозможных пар элементов, где первым берется элемент из первого множества, а вторым – из второго множества. Аналогично задается произведение из нескольких множеств.
Каждый элемент прямого произведения является упорядоченным множеством нескольких элементов: 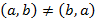 . Такой упорядоченный набор называют вектором в обобщенном виде, элементы которого не обязательно числовые.
. Такой упорядоченный набор называют вектором в обобщенном виде, элементы которого не обязательно числовые.
Для векторного произведения следующего вида

Мощность равна произведению мощностей сомножеств.
Если комбинация состоит из упорядоченного набора элементов, где первый берется из множества мощностью 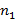 , второй из множества мощностью
, второй из множества мощностью 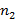 и последний из множества мощностью
и последний из множества мощностью 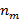 , тогда количество таких комбинаций
, тогда количество таких комбинаций

Любой набор из n элементов без их повторений называют перестановкой этих элементов. Для нахождения числа перестановок учитывается, что на первой позиции может оказаться любой из n элементов, на второй из 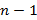 элементов и так далее. Таким образом, число перестановок из n элементов равно
элементов и так далее. Таким образом, число перестановок из n элементов равно 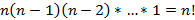 . Обратим внимание, что задачи оптимизации с прямым перебором всех возможных комбинаций обычно сводится к факториалу числа.
. Обратим внимание, что задачи оптимизации с прямым перебором всех возможных комбинаций обычно сводится к факториалу числа.
Если допустимо любое число повторений среди n элементов и на каждой позиции может быть любой из k штук элементов, тогда таких комбинаций 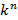 . Если для каждой позиции допустимо свое число повторений, тогда совпадают комбинации с их перестановкой и необходимо разделить факториал на их количество.
. Если для каждой позиции допустимо свое число повторений, тогда совпадают комбинации с их перестановкой и необходимо разделить факториал на их количество.
Пусть имеется n различных элементов, из которых выбирается k штук 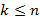 и располагаются подряд, такой упорядоченный ряд называют размещением и находится аналогично перестановке
и располагаются подряд, такой упорядоченный ряд называют размещением и находится аналогично перестановке 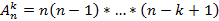 . Для упрощения результата домножим и разделим факториал числа элементов, тогда получим число размещений
. Для упрощения результата домножим и разделим факториал числа элементов, тогда получим число размещений
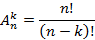
Число размещений дает количество векторов длиной k с различными элементами, которые можно получить из элементов множества мощностью n.
Если из n элементов берется k штук без учета порядка их следования, тогда такую комбинацию называют сочетанием элементов. Сочетание k элементов меньше числа их размещений в 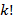 раз. В общем случае сочетание элементов равно
раз. В общем случае сочетание элементов равно
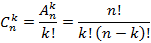
Для конечного множества A мощностью n число сочетаний по k дает количество различных подмножеств с мощностью k. При небольших n число сочетаний удобно находить по треугольнику Паскаля
| 1 | ||||||
| 1 | 1 | |||||
| 1 | 2 | 1 | ||||
| 1 | 3 | 3 | 1 | |||
| 1 | 4 | 6 | 4 | 1 | ||
| 1 | 5 | 10 | 10 | 5 | 1 |
Для любого внутреннего элемента треугольника он равен сумме стоящих выше его элементов. Для нахождения числа сочетаний из n по k сначала выбирается строка, в которой берем элемент с номером k, начиная с 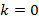 .
.
Сумма элементов каждой строки треугольника дает число всех подмножеств для конечного множества. Каждое множество мощностью n имеет 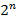 различных подмножеств. Число сочетаний применяется в биноме Ньютона, который имеет следующий вид
различных подмножеств. Число сочетаний применяется в биноме Ньютона, который имеет следующий вид

Множества чисел
Кроме рассмотренных выше конечных множеств можно встретить и бесконечные множества, которые бывают двух основных видов:
1. Множество называется счетным, если возможно каждый его элемент пронумеровать натуральным числом;
2. Множество является несчетным, если нумерация всех его элементов невозможна.
Основными числовыми множествами являются: 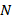 – множество натуральных чисел (ноль не входит),
– множество натуральных чисел (ноль не входит), 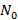 – множество натуральных чисел с включением нуля,
– множество натуральных чисел с включением нуля, 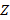 – множество целых чисел. В указанных множествах элементы можно пронумеровать и каждому целому числу соответствует натуральное число, мощности этих множеств совпадают.
– множество целых чисел. В указанных множествах элементы можно пронумеровать и каждому целому числу соответствует натуральное число, мощности этих множеств совпадают.
Множество рациональных чисел 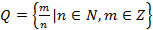 . Упорядочив такие дроби по возрастанию знаменателей, тогда можно выполнить нумерацию натуральными числами, которая также является взаимно-однозначной. Доказано, что любое рациональное число в десятичной форме имеет в дробной части период.
. Упорядочив такие дроби по возрастанию знаменателей, тогда можно выполнить нумерацию натуральными числами, которая также является взаимно-однозначной. Доказано, что любое рациональное число в десятичной форме имеет в дробной части период.
Множество иррациональных чисел I, которые в десятичном виде имеют не периодическую дробную часть, среди которых существуют трансцендентные числа – не являются корнями ни для каких многочленов и нетрансцендентные – числа, являющиеся корнями для некоторых многочленов.
Множество действительных чисел R – множество всех чисел и с периодической и непериодической дробной частью такое, что 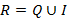 . Часто встречаются подмножества для R в виде
. Часто встречаются подмножества для R в виде 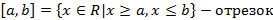 ;
; 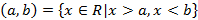 – интервал;
– интервал;  – полуинтервалы и
– полуинтервалы и  – лучи. Возможны объединения этих подмножеств.
– лучи. Возможны объединения этих подмножеств.
Комплексные числа  . Все рассмотренные выше числовые множества являются подмножеством для множества комплексных чисел, поскольку все действительные числа являются комплексными с нулевой мнимой частью.
. Все рассмотренные выше числовые множества являются подмножеством для множества комплексных чисел, поскольку все действительные числа являются комплексными с нулевой мнимой частью.
Теорема: Множество 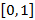 не является счетным.
не является счетным.
Для конечного множества его мощность – число различных элементов, для бесконечных множеств их мощность называют кардиналом. По теореме Кантора мощность отрезка отличается от мощности натуральных чисел
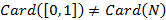
Пусть между счетным и континуальным множествами не существует множеств промежуточной мощности. При этом  является счетным множеством, но
является счетным множеством, но 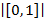 стремится к континууму, является множеством несчетных множеств.
стремится к континууму, является множеством несчетных множеств.
Для доказательства равномощности бесконечных множеств необходимо установить взаимно-однозначное соответствие между их элементами. Бинарные отношения или соответствие на множествах X и Y являются декартовым произведением их подмножеств. Соответствие является функциональным, если для каждого X однозначно определен элемент из Y.
Функциональное соответствие является взаимообратным, если каждому элементу из Y соответствует единственный элемент из X. При выполнении этого для декартового произведения можно утверждать, что для  найдем
найдем 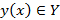 и для
и для 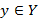 найдется его прообраз
найдется его прообраз  . Именно такое определение функции и взаимо-однозначного взаимодействия вводится в математическом анализе, где X и Y являются числовыми множествами.
. Именно такое определение функции и взаимо-однозначного взаимодействия вводится в математическом анализе, где X и Y являются числовыми множествами.
Множества N, Q и Z равномощны, поскольку между ними можно установить взаимо-однозначное соответствие

Континуальные множества 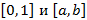 – равномощны, также, как и любые два отрезка числовой оси или плоскости и имеют континуальную мощность. Исключение границ не влияет на мощность – интервал и полуинтервал обладают континуальной мощностью.
– равномощны, также, как и любые два отрезка числовой оси или плоскости и имеют континуальную мощность. Исключение границ не влияет на мощность – интервал и полуинтервал обладают континуальной мощностью.
R и  – равномощны с учетом того, что
– равномощны с учетом того, что 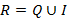 , счетности Q и несчетности R, следует, что I – несчетное множество. Тем самым мощность иррациональных чисел существенно превосходит мощность рациональных.
, счетности Q и несчетности R, следует, что I – несчетное множество. Тем самым мощность иррациональных чисел существенно превосходит мощность рациональных.
Объединением и пересечением конечного числа и конченого множества получим конечное множество. Для счетных множеств объединение дает счетное множество. Для конечного множества A множеством его подмножеств имеет 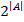 – мощность. Для счетного множества число всех его подмножеств континуально.
– мощность. Для счетного множества число всех его подмножеств континуально. 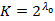 – описывает связь мощности счетного и несчетного множеств.
– описывает связь мощности счетного и несчетного множеств.
Мощность объединений множеств 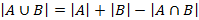 . Для пересекающихся множеств
. Для пересекающихся множеств  . В общем случае мощность объединения n множеств определяет формулу включения-исключения
. В общем случае мощность объединения n множеств определяет формулу включения-исключения
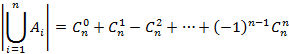
Операции с числами
Операции над числами – совокупность действий над упорядоченной последовательностью цифр в соответствии с набором правил, задаваемых алгоритмами выполнения операций, в результате которых образуется новая последовательность цифр. Основными операциями над числами являются арифметические операции, операции сравнения, преобразования числа и логические операции.
К арифметическим операциям относятся операции сложения, вычитания, умножения, деления и извлечение квадратного корня. Методы выполнения этих операций зависят от класса числа – числового множества. Комплексное число представляет собой упорядоченную пару вида  , геометрически комплексное число располагается на плоскости, в отличии от всех остальных чисел, которые располагаются на прямой.
, геометрически комплексное число располагается на плоскости, в отличии от всех остальных чисел, которые располагаются на прямой.
Алгебраические операции над комплексными числами производятся иначе, чем над всеми остальными числами. Простейшие алгебраические операции над комплексными числами:
1. Сложение: 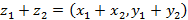 ;
;
2. Вычитание: 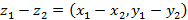 ;
;
3. Умножение на действительное число: 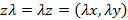 ;
;
Остальные алгебраические действия над комплексными числами производится в алгебраической форме записи комплексного числа вида 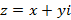
1. Умножение:  ;
;
2. Деление: 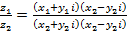 .
.
Помимо основных алгебраических операций и алгебраической формы у комплексных чисел определена операция сопряжения вида 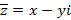 , которая представляет собой смену знака между действительной и мнимой частью. В тригонометрической форме комплексного числа вида
, которая представляет собой смену знака между действительной и мнимой частью. В тригонометрической форме комплексного числа вида  определены следующие операции
определены следующие операции
1. Умножение
 ;
;
2. Возведение в степень (формула Муавра)

3. Деление
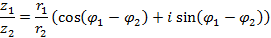
4. Извлечение корня натуральной степени
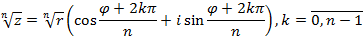
5. Извлечение корня комплексной степени (производится в показательной форме комплексного числа)

Комплексные числа на ровне со всеми другими способны определять собственные множества на z-плоскости. Пусть имеется два комплексных числа, тогда соотношение следующего вида 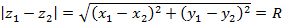 задает окружность с центром в точке
задает окружность с центром в точке 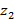 с радиусом R. Общее уравнение кривой на z-плоскости задается соотношением следующего вида
с радиусом R. Общее уравнение кривой на z-плоскости задается соотношением следующего вида 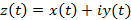 , которая может быть как ориентированной, так и не ориентированной.
, которая может быть как ориентированной, так и не ориентированной.
Комплексный многочлен – выражение следующего вида, в котором учувствуют только комплексные числа и переменные

Любой комплексный многочлен n-ой степени можно представить в следующем виде, в котором  – корни многочлена, а
– корни многочлена, а  – кратности со свойством
– кратности со свойством 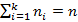

Если у комплексного многочлена все коэффициенты действительные, тогда комплексные корни будут встречаться сопряженными парами.
 2020-08-05
2020-08-05 236
236








