2020-09-24
110
1. Привести все одночлены к стандартному виду.
2. Убедиться, что все одночлены подобны; если же они не подобны, то алгоритм далее не применяется.
3. Найти сумму коэффициентов подобных одночленов.
4. Записать ответ: одночлен подобный данным, с коэффициентом, полученным на третьем шаге.
Многочлены. Арифметические операции над многочленами.
1. Многочленом называют сумму одночленов.
2. Слагаемые (одночлены), из которых состоит многочлен, называют членами многочлена.
3. Если в многочлене все члены записаны в стандартном виде и приведены подобные члены, то говорят, что многочлен приведен к стандартному виду.
4. Чтобы записать алгебраическую сумму нескольких многочленов в виде многочлена стандартного вида, нужно раскрыть скобки и привести подобные члены.
5. Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен и полученные произведения сложить.
6. Чтобы умножить многочлен на многочлен, нужно умножить каждый член одного многочлена поочерёдно на каждый член другого многочлена и полученные произведения сложить.
|
|
|
7. Квадрат суммы двух выражений равен сумме их квадратов плюс их удвоенное произведение. 
= 
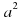+2аб+ 
8. Квадрат разности двух выражений равен сумме их квадратов минус их удвоенное произведение.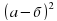 
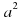= -2аб+
9. Разность квадратов двух выражений равна произведению суммы этих выражений на их разность. 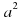- = (а- б)(а+ б).
10. Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.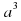 
- 
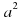= (а- б)( + аб+ ).
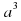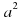11. Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности. + = (а + б)( - аб+ ).
12. Чтобы разделить многочлен на одночлен, нужно каждый член многочлена разделить на этот одночлен и полученные результаты сложить.
