Тема: Правило Лопиталя для вычисления пределов

Цель: сформировать умение применять правило Лопиталя для нахождения пределов.

Теоретические сведения к практическому занятию

Правило Лопиталя. Предел отношения двух б.м. 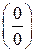 или б.б.  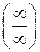функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:

                                                                         (*)

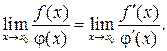Чтобы использовать правило Лопиталя для раскрытия неопределённостей других типов, выражение под знаком предела следует преобразовать

16

элементарными способами так, чтобы получить неопределенность 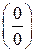 или 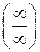 и затем использовать формулу (*).

Пример 1. Найти пределы, используя правило Лопиталя или элементарные способы раскрытия неопределённостей:

  а) 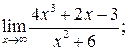   б)  

Решение.

а) Подставляя в функцию вместо х предельное значение 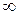, определим предел числителя и знаменателя.

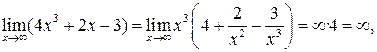 т. к.

Аналогично: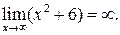

Имеем неопределенность вида 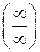. Используем правило Лопиталя:

б)

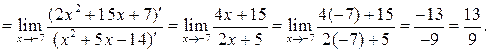
Самостоятельная работа:

Задание 1. Найти пределы, используя правило Лопиталя.

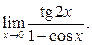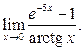1)   2)      3)

 

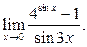
Содержание практического занятия:

А. Ответить на вопросы:

1) В чем заключается правило Лопиталя. В каких случаях оно употребляется?

2) Как использовать правило Лопиталя для раскрытия неопределенностей различных типов?

3) Приведите примеры использования правила Лопиталя для раскрытия неопределенностей различных типов.

Б. Выполнить задания:

Задание 1. Найти пределы, используя правило Лопиталя.

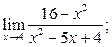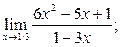1)  2)       3)

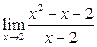
Задание 2. Найти пределы, используя правило Лопиталя.

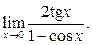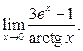1)   2)      3)

 

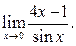
Тема: Неопределенный интеграл. Таблица интегралов.

Цель: сформировать умение вычислять неопределенные интегралы, знать таблицу основных интегралов.