2020-09-24
136
Связь между декартовыми и полярными координатами:
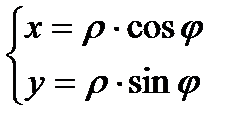, где 
.
Вычислим якобиан перехода
.
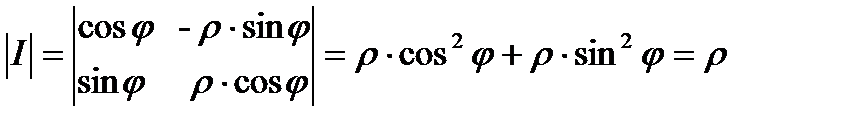Таким образом, получаем равенство:
.
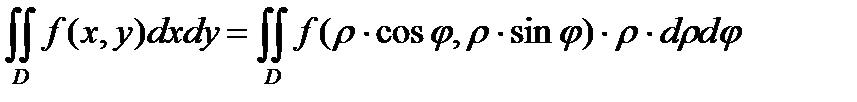Замечания:
1) К полярным координатам удобно переходить в том случае, если область D ограничена дугами окружности и лучами.
2) При переходе к полярным координатам надо следить за тем, чтобы и границы области, и подынтегральная функция имели в полярных координатах простой вид.
3 случая расположения области D:
1) Полюс находится вне области D и любой луч, проведенный из полюса, пересекает границу области не более чем в двух точках.
.
2) Полюс находится внутри области D и любой луч, выходящий из полюса пересекает границу области только в одной точке.
.
3) Полюс находится на границе области.
.
Пример. Вычислить двойной интеграл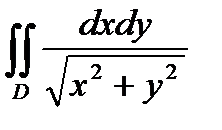 
, где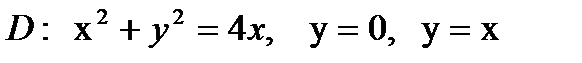 
.
, 
― окружность с центром (2;0) и радиусом R=2.
Построим область D.
Перейдем к полярным координатам.
Запишем уравнение окружности в полярных координатах:
: 
, 
, 
.
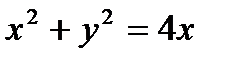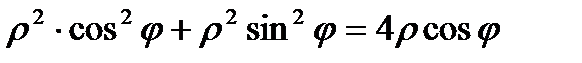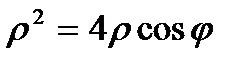Запишем подынтегральную функцию в полярных координатах:
.
.
;
.
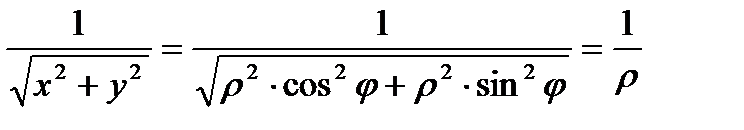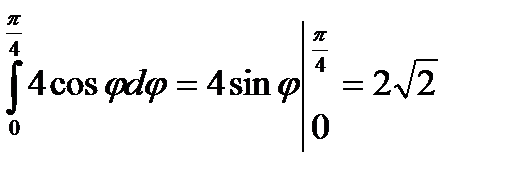Применение двойного интеграла.
1. Вычисление объема цилиндрического тела.
Цилиндрическое тело ограничено областью D на плоскости (x,y), а сверху поверхностью z=f(x,y).
.
Пример. Вычислить объем тела, ограниченного поверхностями:
x=0 – плоскость yz,
y=0 – плоскость zx,
z=0 – плоскость xy,
x=2 – плоскость, параллельная yz,
y=3 – плоскость, параллельная zx,
z=x2+y2 – эллиптический параболоид – сверху.
.
;
.
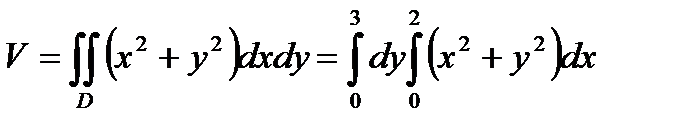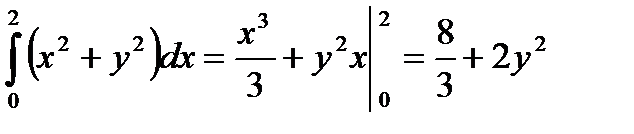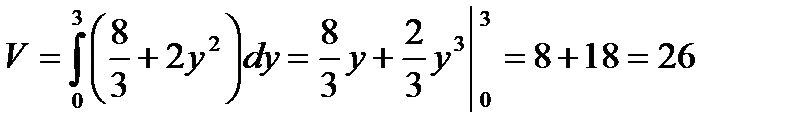2. Вычисление площади плоской фигуры.
Если фигура ограничена областью D на плоскости (x,y), то ее площадь: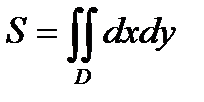 
.
Пример. Вычислить площадь плоской фигуры, ограниченной линиями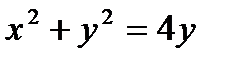 
, 
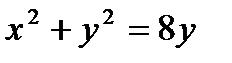, y=x, 
.
.
.
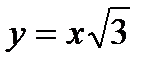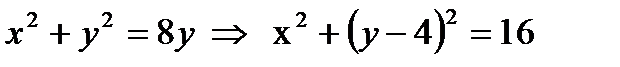Перейдем к полярным координатам:
.
; 
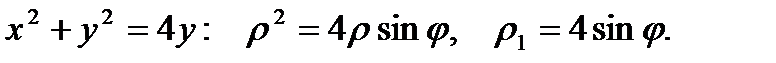
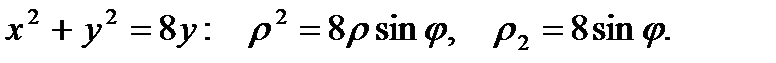
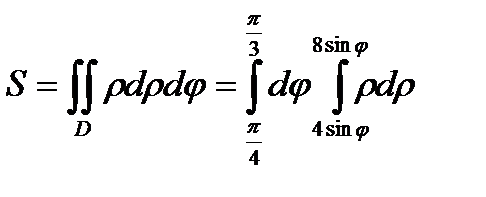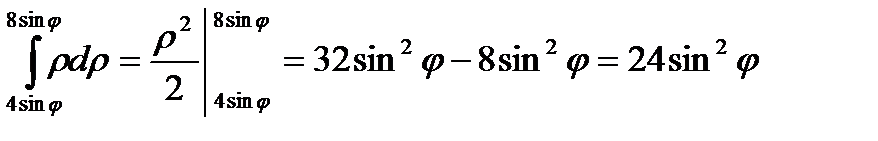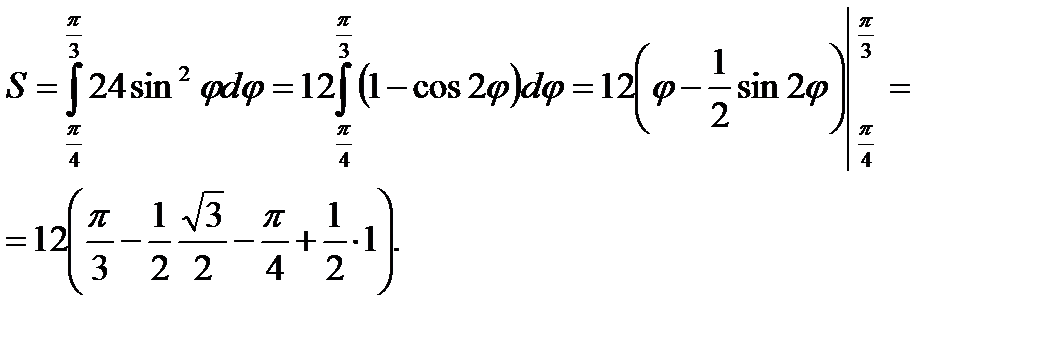
3. Если поверхностная плоскость задается функцией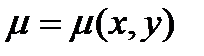 
, тогда с помощью двойного интеграла можно найти массу плоской пластины
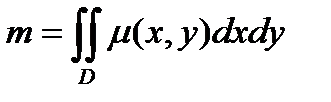, где D – область, которую занимает данная пластина.
