Поверхности второго порядка

I. Цилиндрическая поверхность.

1) Эллиптический цилиндр .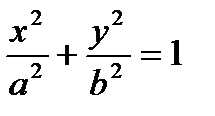

Направляющей является эллипс в плоскости xy, а образующие параллельны оси z.

2) Параболический цилиндр z=x²

Направляющей будет являться парабола в плоскости xz, а образующие параллельны оси y.

3) Гиперболический цилиндр .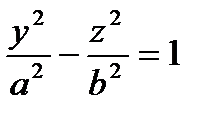

Направляющей является гипербола в плоскости yz, а образующие параллельны оси x.

II. Эллипсоид . Если а=в=с, то получаем сферу.

III. Двуполостный гиперболоид .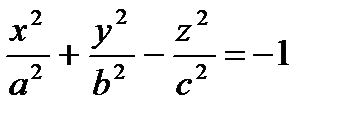

Плоскость xy данную поверхность не пересекает, т. к. получаем при z=0 .

IV. Конус .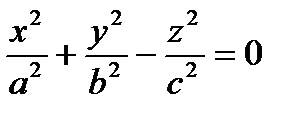

Плоскость xy данную поверхность пересекает только в начале координат.

V. Эллиптический параболоид .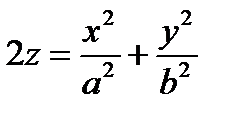

Данная поверхность пересекает плоскость xy только в начале координат.

 

Задача о массе неоднородного тела.

Пусть дано тело, ограниченное замкнутой поверхностью Т, причем плотность в каждой ее точке зависит от координат этой точки . Требуется найти массу данного тела. Разобьем все тело на п частей. Пусть - объем i -ой части. В каждой части произвольно выберем точку 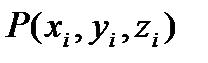 и предположим, что плотность каждой i -ой части постоянна и равна значению в точке Р. Тогда масса i -ой части 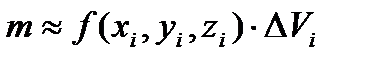. Тогда масса всего тела 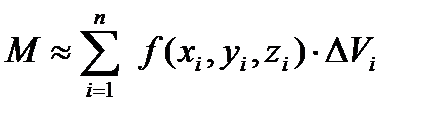. Данное равенство тем точнее, чем на большее число частей мы разбиваем тело .

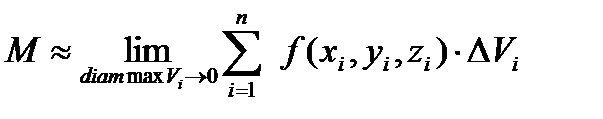Дадим общее определение, не связанное с физическими или геометрическими свойствами.

 

Определение тройного интеграла.

Пусть дана область Т, в каждой точке которой определена непрерывная функция U=f(x,y,z). Разобьем область Т произвольно на п частей и обозначим  - объем i -ой части. На каждом участке разбиения произвольно выберем точку 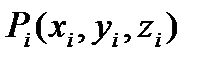 и составим интегральную сумму .

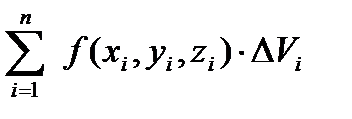Если существует конечный предел интегральной суммы, не зависящий ни от способа разбиения области Т на части, ни от выбора точек P_i, тогда этот предел называется тройным интегралом по области Т от функции f(x,y,z).

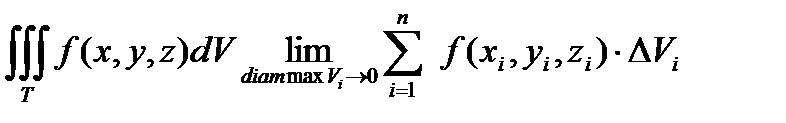, где dV – элемент объема.