Рассмотрим правильную дробь  , где
, где  – многочлен степени n. Будем считать, что старший коэффициент в
– многочлен степени n. Будем считать, что старший коэффициент в 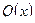 равен единице. В курсе алгебры доказывается, что такой многочлен с действительными коэффициентами может быть разложен на множители первой и второй степени с действительными коэффициентами:
равен единице. В курсе алгебры доказывается, что такой многочлен с действительными коэффициентами может быть разложен на множители первой и второй степени с действительными коэффициентами:
 ,
,
где  - действительные корни многочлена
- действительные корни многочлена 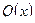 , а квадратные трёхчлены не имеют действительных корней. Можно доказать, что тогда
, а квадратные трёхчлены не имеют действительных корней. Можно доказать, что тогда  представляется в виде суммы простейших дробей I-IV:
представляется в виде суммы простейших дробей I-IV:


 ,
,
где показатели у знаменателей последовательно уменьшаются от  до 1,
до 1, 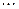 , от
, от  до 1, от
до 1, от  до 1,
до 1, 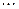 , от
, от  до 1, а
до 1, а  ,
, 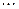 ,
,  - неопределённые коэффициенты.
- неопределённые коэффициенты.
Методы нахождения неопределённых коэффициентов
1) Метод частных значений:

Тогда  .
.
Придаём x переменной определённые значения (корни знаменателя) и находим коэффициенты A и B:
 :
:  ,
, 
 :
:  ,
, 
В качестве частных значений берём корни знаменателя, получаем:



2) Метод сравнения коэффициентов:

Получаем  .
.
Даём x значение, равное действительному корню знаменателя:
 :
:  ,
, 
Сравниваем коэффициенты при одинаковых степенях x:
при  :
:  .
.
при  :
:  .
.

Получаем




Тема 12. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ И ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
 2020-09-24
2020-09-24 93
93








