Мощным средством исследования в математике, физике, механике и других дисциплинах является определённый интеграл – одно из основных понятий математического анализа. С его помощью вычисляются площади, длины дуг, объёмы, работа, скорость и т.д.
Пусть на отрезке  задана непрерывная функция
задана непрерывная функция 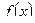 . Обозначим через
. Обозначим через  и
и 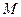 её наименьшее и наибольшее значения на этом отрезке.
её наименьшее и наибольшее значения на этом отрезке.
Разобьём отрезок  на
на  частей точками деления
частей точками деления
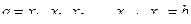 ,
,
причём 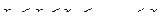 .
.
Положим 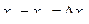 ,
,  ,...,
,..., 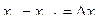 .
.
Обозначим наибольшее и наименьшее значения функции 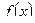 :
:
на отрезке 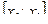 через
через 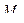 и
и 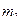 ;
;
на отрезке 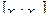 через
через 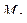 и
и 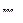 ;
;
на отрезке 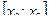 через
через 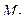 и
и 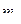 ;
;
на отрезке 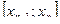 через
через 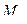 и
и 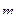 .
.

Составим суммы:
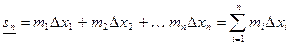 , (1)
, (1)
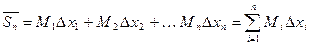 . (2)
. (2)
Сумма 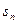 называется нижней интегральной суммой, а сумма
называется нижней интегральной суммой, а сумма 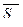 называется верхней интегральной суммой.
называется верхней интегральной суммой.
Если 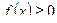 , то нижняя интегральная сумма численно равняется площади «вписанной ступенчатой фигуры», а верхняя интегральная сумма численно равняется площади «описанной ступенчатой фигуры».
, то нижняя интегральная сумма численно равняется площади «вписанной ступенчатой фигуры», а верхняя интегральная сумма численно равняется площади «описанной ступенчатой фигуры».
Свойства верхних и нижних интегральных сумм.
1. Так как 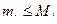 , где
, где 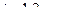 , то
, то 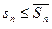 (на основании формул (1) и (2)).
(на основании формул (1) и (2)).
2. Так как 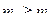 ,
, 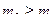 ,
, 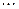 ,
, 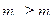 , где
, где  – наименьшее значение
– наименьшее значение 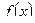 на
на  , то
, то
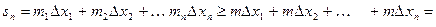
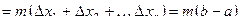 .
.
Таким образом, 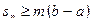 .
.
3. 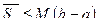 , где
, где 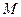 - наибольшее значение
- наибольшее значение 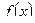 на
на  .
.
Доказательство: Так как 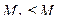 ,
, 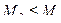 ,
, 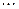 ,
, 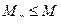 , то
, то
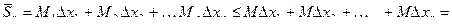
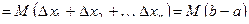 .
.
Таким образом, 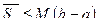 .
.
Из свойств 2 и 3 следует
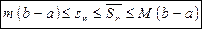 .
.
 2020-09-24
2020-09-24 208
208








