Интегрирование методом замены переменной

Пусть требуется найти интеграл 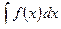, причём непосредственно подобрать первообразную для  мы не можем, но нам известно, что она существует.

Сделаем замену переменной в подынтегральном выражении, положив

,

где  - непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда  и имеет место равенство:

.                                  (7)

Формула (7) называется формулой замены переменной под знаком неопределённого интеграла.

Пример:

Делаем замену , тогда , .

Замечание. При интегрировании иногда целесообразно подбирать замену переменной в виде не , а . Пусть, например, требуется вычислить интеграл . В результате подстановки ,  получаем:

.

Пример:

Замена: , .

 

Интегрирование по частям

Формула интегрирования по частям имеет следующий вид:

 .

Этой формулой обычно пользуются, когда подынтегральное выражение  проще, чем подынтегральное выражение .

Пример:

Замечание. При нахождении 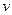 не пишут промежуточную произвольную постоянную , так как она не оказывает влияния на окончательный результат.

Пример:

Правило интегрирования по частям применяется во многих случаях, например, для интегралов вида

,          ,

,               ,                 ,

а также для некоторых интегралов, содержащих логарифмическую, обратные тригонометрические функции и корни.

 

Тема 11. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ