Определение 2. Совокупность всех первообразных для функции 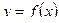 на промежутке X называется неопределённым интегралом от функции
на промежутке X называется неопределённым интегралом от функции 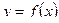 на X и обозначается
на X и обозначается 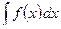 . Функция
. Функция 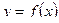 называется подынтегральной функцией для
называется подынтегральной функцией для 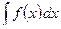 , а произведение
, а произведение 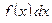 называется подынтегральным выражением.
называется подынтегральным выражением.
Таким образом,
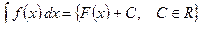 .
.
На практике принята более короткая запись:
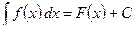 .
.
Свойства неопределённого интеграла.
1. Производная от неопределённого интеграла равна подынтегральной функции, т.е. если 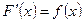 , то и
, то и
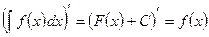 .
.
Последнее равенство следует понимать в том смысле, что производная от любой первообразной равна подынтегральной функции.
2. Дифференциал от неопределённого интеграла равен подынтегральному выражению
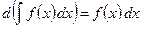 .
.
3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
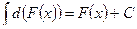 .
.
В частности, 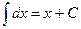 , где
, где 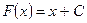 .
.
4. Неопределённый интеграл от алгебраической суммы (разности) двух или нескольких функций равен сумме (разности) их интегралов:
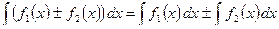 .
.
5. Постоянный множитель можно выносить за знак интеграла, т.е. если a=const, то
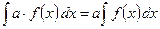 .
.
Таблица интегралов
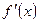
| 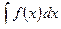
| |
| 1. | 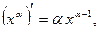
| 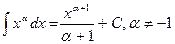
|
| 2. | 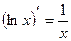
| 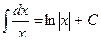
|
| 3. | 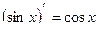
| 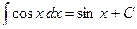
|
| 4. | 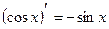
| 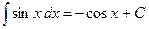
|
| 5. | 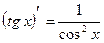
| 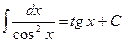
|
| 6. | 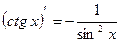
| 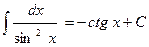
|
| 7. | 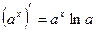
| 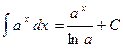
|
| 8. | 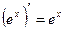
| 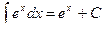
|
| 9. | 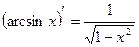
| 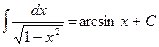
|
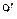 . .
| 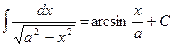
| |
| 10. | 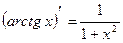
| 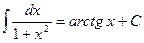
|
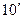 . .
| 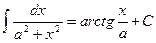
| |
| 11. | 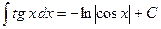
| |
| 12. | 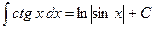
| |
| 13. | 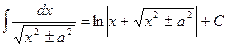
|
Метод вычисления интегралов, при котором они сводятся к табличным путём применения к ним основных свойств неопределённых интегралов, называется непосредственным интегрированием.
Примеры:
1) 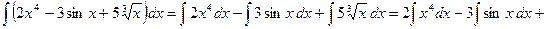
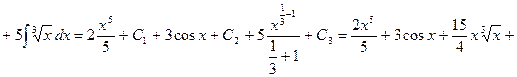
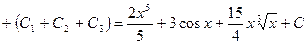
2) 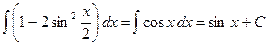
Используем формулу: 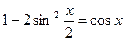 .
.
При вычислении неопределённого интеграла часто применяется следующее правило:
Если 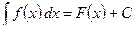 , то
, то 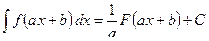 .
.
Примеры:
1) 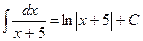
2) 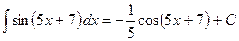
 2020-09-24
2020-09-24 339
339








