Интегрирование некоторых классов тригонометрических функций

 

Рассмотрим интегралы от некоторых классов тригонометрических функций. Покажем, что интеграл вида

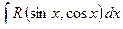                                           (1)

с помощью подстановки 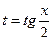 всегда сводится к интегралу от рациональной функции.

;

,

.

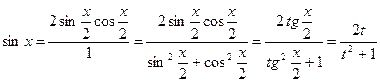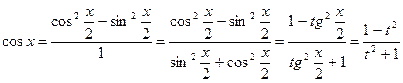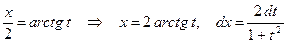Таким образом, ,  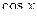и 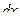 выразились рационально через t. Подставляя полученные выражения в (1), приходим к интегралу от рациональной функции:

.

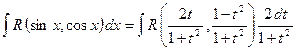Пример:

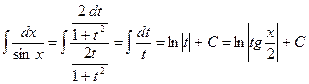
подстановка: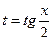

                  

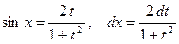
Рассмотренная подстановка даёт возможность проинтегрировать всякую функцию вида 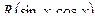. Поэтому она называется «универсальной тригонометрической подстановкой». Однако на практике она часто приводит к слишком сложным рациональным функциям, поэтому применяются другие тригонометрические подстановки.

1) Если интеграл имеет вид 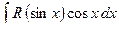, то используется подстановка 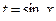, , 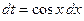в результате которой получаем .

2)

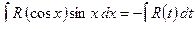
подстановка: ,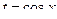

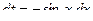
3)

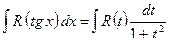
подстановка: , ,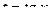

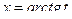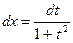
4) Если подынтегральная функция имеет вид 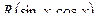, но  и 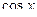 входят в выражение только в чётных степенях, то применяется та же подстановка 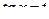, тогда

, , .

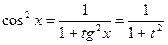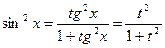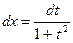После подстановки мы получим интеграл от рациональной функции.

Примеры:

1)

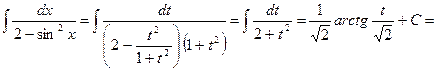
(используем подстановку )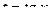

2)

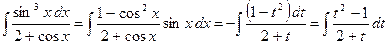
Используем подстановку .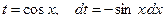

Выделяем целую часть дроби 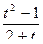, в результате получаем 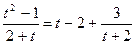. Тогда

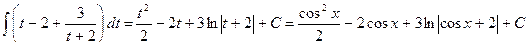
5)

а) m или n – нечётное число, пусть, например, 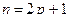, тогда

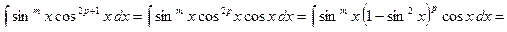
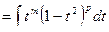
(подстановка: )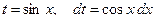

Таким образом, получен интеграл от рациональной функции.

Пример:

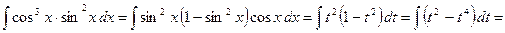
подстановка: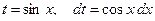

б) 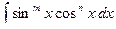, где m и n - числа неотрицательные и чётные, т.е. 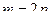, , 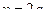тогда

Пример:

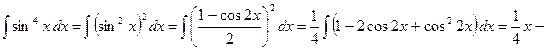
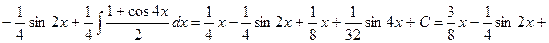
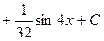
в) Если m и n – чётные и одно из этих значений – отрицательное, используем подстановку 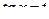 (или 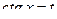), как в случае 4.

Пример:

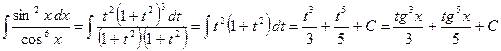
(подстановка: )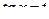

6) ,     ,    

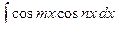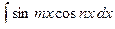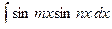
Интегралы берутся при помощи тригонометрических формул:

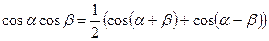
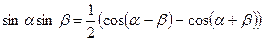
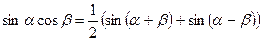
Пример:

 

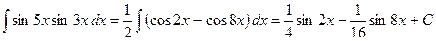
РАЗДЕЛ 4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

 

Тема 13. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА