Вариант 2
1. Прямая называется перпендикулярной к плоскости, если она перпендикулярна…
1) к одной прямой, лежащей в плоскости;
2) к двум прямым, лежащим в плоскости;
3) к любой прямой, лежащей в плоскости.
2. 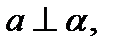
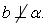
Тогда прямые a и b не могут быть…
1) перпендикулярными;
2) параллельными;
3) скрещивающимися.
3. Диагональ АС квадрата ABCD перпендикулярна некоторой плоскости 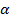
, проходящей через точку А. Тогда диагональ BD …
1) перпендикулярна плоскости 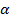 ;
;
2) параллельна плоскости 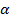 ;
;
3) лежит в плоскости 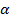 .
.
4. ABCD – параллелограмм, 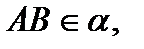
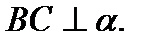 Тогда ABCD не может быть…
Тогда ABCD не может быть…
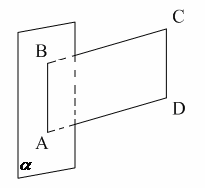
1) ромбом;
2) квадратом;
3) прямоугольником.
5. 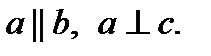 Прямые b и с не могут быть…
Прямые b и с не могут быть…
1) параллельными;
2) перпендикулярными;
3) скрещивающимися.
6. Какое утверждение неверное?
1) Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
2) Через точку, не лежащую на данной прямой, можно построить только одну плоскость, перпендикулярную данной прямой.
3) Через точку, не лежащую на данной прямой, можно построить только одну прямую, перпендикулярную данной прямой.
КЛЮЧИ К тестУ по теме: «Перпендикулярные прямые в пространстве. Перпендикулярность прямой и плоскости»
| № п/п вариант | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 3 | 1 | 2 | 3 | 1 | 2 |
| 2 | 3 | 2 | 2 | 1 | 1 | 3 |
ТЕМА 4. Перпендикулярность прямых и плоскостей
Вариант 1
| В заданиях А1 – А5 необходимо выбрать один правильный ответ. | ||
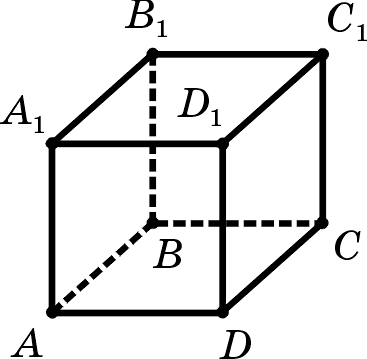
| А1 | В кубе АВСDА1В1С1D1 укажите плоскости, перпендикулярные прямой ВС: |
|
| а) АВВ1 и DСС1; б) АDD1 и ВСС1; в) АСС1 и ВDD1; г) АВС и А1В1С1. | ||
| А2 | В кубе АВСDА1В1С1D1 укажите проекцию прямой В1D на плоскость ADD1: |
|
| а) AD; б) D1D; в) D1А1; г) А1D. | ||
| А3 | В кубе АВСDА1В1С1D1 расстояние между прямыми В1С и АА1 определяется как длина отрезка: |
|
| а) А1С; б) АВ1; в) А1В1; г) АС. | ||
| А4 | В кубе АВСDА1В1С1D1 углом между прямой В1D и плоскостью В1АА1являетсяугол: |
|
| а) А1В1А; б) АВ1В; в) АВ1D; г) А1В1D. | ||
| А5 | В кубе АВСDА1В1С1D1 линейным углом двугранного угла DАА1С1 является угол: |
|
| а) С1АD; б) САD1; в) С1А1D; г) САD. | ||
| В задании А6 – А7 необходимо выбрать верные утверждения. Для каждого утверждения укажите: верно (+) или не верно (–). | ||
| А6 | Если в пространстве дана прямая а и точка А вне ее, то: | |
| 1) Через точку А можно провести только одну прямую, которая перпендикулярна прямой a и пересекает ее. 2) Через точку А можно провести бесконечное множество прямых, перпендикулярных прямой a. 3) Через точку А можно провести две различные плоскости, которые перпендикулярны прямой a. 4) Через точку А можно провести только одну плоскость, перпендикулярную прямой a. | верно / не верно верно / не верно верно / не верно верно / не верно | |
| А7 | В кубе АВСDА1В1С1D1 проведено сечение плоскостью АВ1С1. Тогда: | 
|
| 1) Плоскость АВВ 1 перпендикулярна линии пересечения секущей плоскости и плоскости ABC. 2) Углом между секущей плоскостью и прямой AB является угол между прямыми AB и AC 1. 3) Угол между секущей плоскостью и плоскостью ABC равенуглу BAB 1. 4) Угол между секущей плоскостью и плоскостью ABC равен 45°. | верно / неверно верно / неверно верно / неверно верно / неверно | |
| В задании А8 необходимо выбрать свойства, которыми обладает прямоугольный параллелепипед. Длякаждогоутвержденияукажите: да (+) илинет (–). | ||
| А8 | 1) Сумма плоских углов при вершине равна 270°. 2) Всетриизмеренияравны. 3) Всеграни – прямоугольники. 4) Диагонали пересекаются в одной точке и делятся этой точкой пополам. 5) Диагоналиперпендикулярныоснованиям. 6) Вседиагоналиравны. | да / нет да / нет да / нет да / нет да / нет да / нет |
| В заданиях В1 – В3 решите задачи, в ответе укажите число без единиц измерения. | ||
| В1 | Проекция наклонной, проведенной из точки А к плоскости, равна | |
| В2 | В треугольнике АВС угол С = 90° и ВС = 6. Отрезок ВD перпендикулярен к плоскости АВС и ВD = 8. Найдитерасстояниеотточки D допрямой АС. | |
| В3 | Найдите диагональ прямоугольного параллелепипеда, если его измерения равны 1; 3; | |
 2020-09-24
2020-09-24 548
548

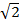 см. Найдитедлинунаклонной, еслионаобразует с плоскостьюугол 45°.
см. Найдитедлинунаклонной, еслионаобразует с плоскостьюугол 45°.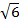 .
.






