Задания для практических работ

Построить линии приёмки и браковки, принимая во внимание, что вероятность отказа подчиняется биномиальному закону для исходных данных в табл. 5.1 и определить среднее число испытаний (n ₀, n ₁). Таблица 5.1

Содержание отчёта

1. Название расчёта, задача и номер варианта;

2. Расчётные формулы с пояснительным текстом;

3. Расчётные формулы с численными значениями;

4. Выводы по работе.

Таблица 5.1

Исходные данные для биномиального закона

№	P 0	P 1	α	β	n 0
1.	0,825	0,8	0,1	0,1	871
2.	0,85	0,8	0,1	0,1	210
3.	0,875	0,8	0,1	0,1	89
4.	0,925	0,8	0,1	0,1	29
5.	0,95	0,8	0,1	0,1	19
6.	0,975	0,8	0,1	0,1	13
7.	0,999	0,8	0,1	0,1	8
8.	0,9	0,85	0,1	0,1	161
9.	0,9	0,825	0,1	0,1	79
10.	0,9	0,875	0,1	0,1	578
11.	0,9	0,925	0,1	0,1	428
12.	0,9	0,95	0,1	0,1	85
13.	0,9	0,975	0,1	0,1	26
14.	0,9	0,999	0,1	0,1	5
15.	0,9	0,8	0,05	0,1	54
16.	0,9	0,8	0,01	0,1	64
17.	0,9	0,8	0,01	0,01	122
18.	0,9	0,8	0,01	0,05	79

 

 

			Продолжение				Табл. 5.1
№	P 0	P 1	α		β		n 0
19.	0,9	0,8		0,05		0,15		50
20.	0,9	0,8		0,01		0,15		43
21.	0,9	0,8		0,1		0,15		38
22.	0,9	0,8		0,15		0,15		33
23.	0,95	0,8		0,05		0,1		22
24.	0,95	0,8		0,01		0,1		24
25.	0,95	0,8		0,01		0,01		48
26.	0,95	0,8	0,01		0,05		31
27.	0,95	0,8	0,05		0,15		17
28.	0,95	0,8	0,01		0,15		19
29.	0,95	0,8	0,1		0,15		15
30.	0,95	0,8	0,15		0,15		13
31.	0,95	0,85	0,15		0,15		24
32.	0,95	0,85	0,05		0,15		32
33.	0,95	0,85	0,15		0,05		42
34.	0,95	0,85	0,1		0,1		47
35.	0,95	0,85	0,01		0,01		89
36.	0,95	0,85	0,05		0,05		52

 

 

 

Планирование испытаний для экспоненциального закона

Экспоненциальный закон распределения времени безотказной работы или функция надёжности определяется формулой:

.

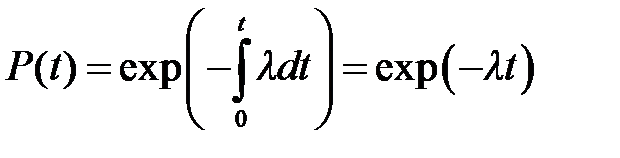(6.1)

Здесь λ – интенсивность отказов (параметр распределения), T = 1/ λ – средняя наработка на отказ.

Если принять, что λ<<0,1, то формула вероятности безотказной работы упрощается в результате разложения в ряд и принимает вид:

.

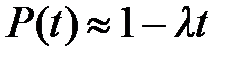(6.2)

Плотность распределения экспоненциального закона описывается выражением

,

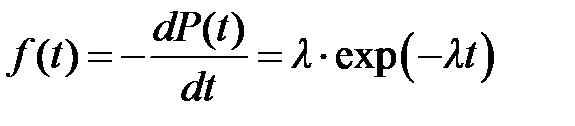(6.3)

а функция распределения – зависимостью вида

.

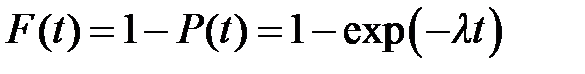(6.4)

Используя логарифм (2.1), можно получить [11, 14]

.

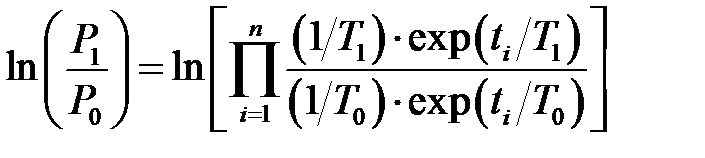(6.5)

Принимая t_i = t, после логарифмирования правой части этого выражения можно получить:

.

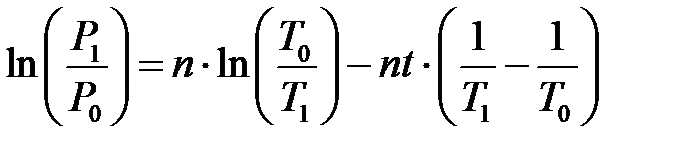(6.6)

Согласно соотношениям (2.12)…(2.16) для принятия или отклонения гипотезы H ₀ в зависимости от полученного числа отказов m можно получить следующие условия принятия гипотезы H ₀:

; ;

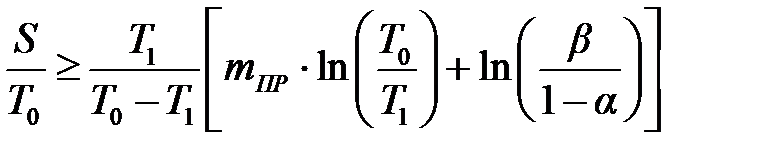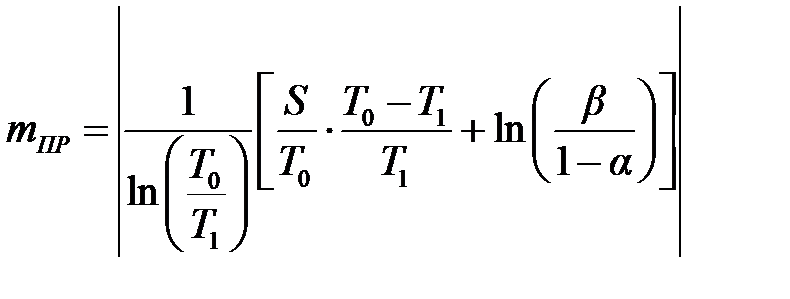(6.7)

отклонения гипотезы H ₀:

; ,

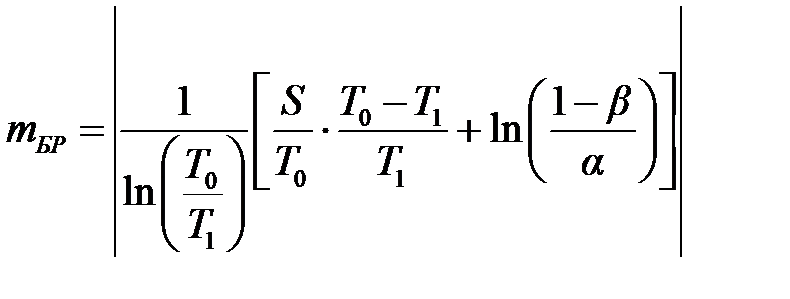(6.8)

где S = nt – общая продолжительность испытаний до наступления m -го отказа; среднее ожидаемое число отказов m и среднее ожидаемое время испытаний S в зависимости от величин T ₀/ T ₁, α и β следует определять по приведённым ниже формулам. Так, для подтверждения того, что T = T ₀, используют следующие формулы:

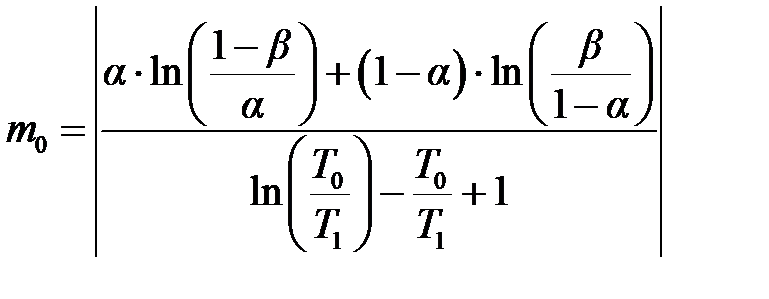,	(6.9)
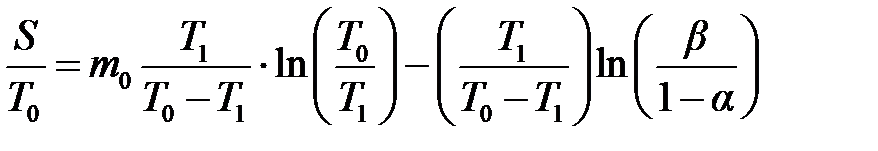,	(6.10)

откуда общая продолжительность испытаний

.

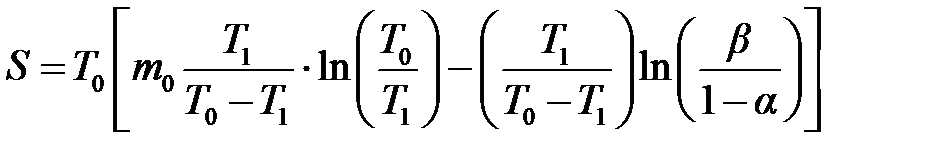(6.11)

Для подтверждения выполнения условий T = T ₁ проводят следующие расчёты:

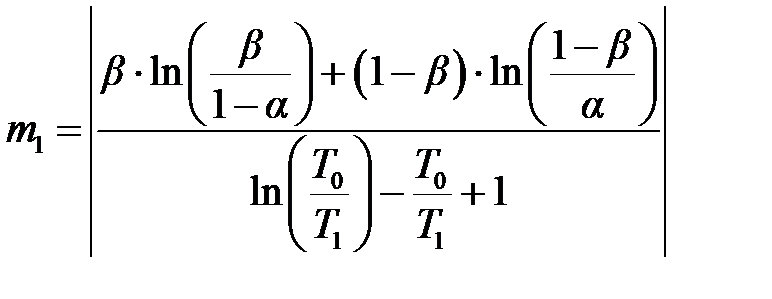,	(6.12)
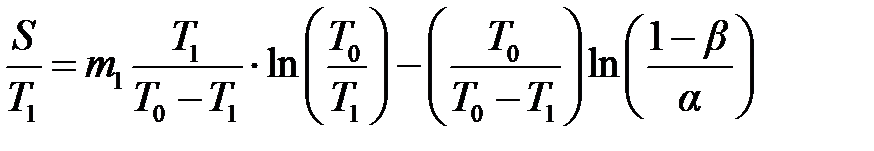,	(6.13)

откуда общая продолжительность испытаний

.

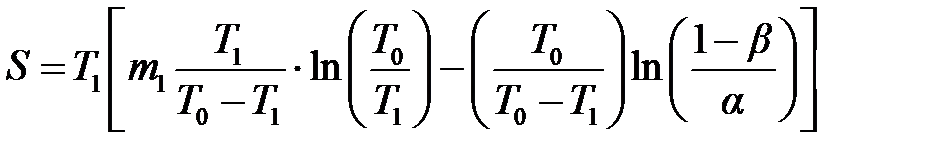(6.14)

 

 

Пример

Задача. Изделие должно обладать наработкой на отказ T ₀ с рисками поставщика и заказчика α = β =0,1, при этом задано отношение T ₀/ T ₁ = 1,2. Требуется построить линии приёмки и браковки изделия по результатам испытаний [11, 14] и определить среднее число испытаний (m ₀, m ₁).

Решение. Для вывода формул линий приёмки и браковки воспользуемся уравнениями (6.7) и (6.8) принятия и отклонения гипотезы H ₀ (рис. 6.1): Рис. 6.1

; ;

; .

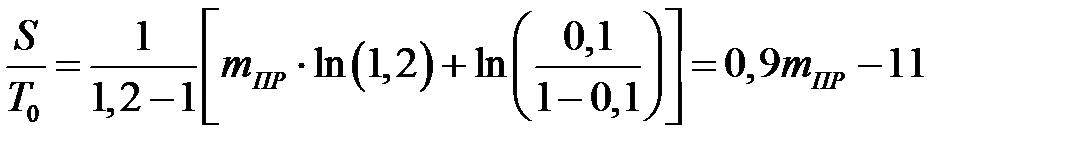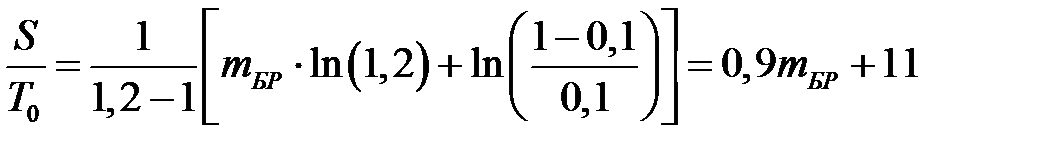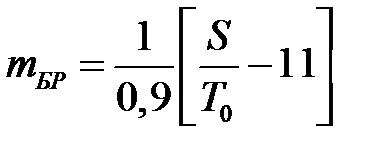Задаваясь значениями S / T ₀, определим m_ПР и m_БР для уровней соответствия и несоответствия изделия этим требованиям.

 

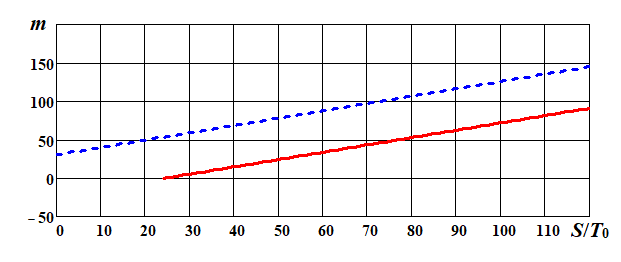
Рис. 6.1. Графики линий приёмки (––) и браковки (- - -) для экспоненциального закона при α = β =0,1; T ₀/ T ₁ = 1,2; m ₀ = 99.

Контрольные вопросы

1. Дайте определение экспоненциальному закону.

2. Поясните отношение правдоподобия для экспоненциального закона.

3. Поясните понятие «средняя наработка на отказ».