2020-09-24
87
Сила, которая будет действовать на произвольный заряд со стороны остальных зарядов, который мы поместим в любую точку в пространства, согласно закону Кулона и принципу суперпозиции (2), пропорциональна величине этого заряда Q. Взяв отношению этой силы к величине заряда можно определить векторное поле, в этой точке пространства равное:
, (3)
где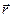 
– координаты точки в которой мы определяем поле 
; 
– координаты заряда qi. Это векторное поле носит название напряжённость электрического поля. Напряжённость - является силовой характеристикой электрического поля, поскольку сила действующая на любой заряд Q, помещённый в поле с величиной напряжённости равна:
. (4)
Фактически, большинство задач электростатики ставят целью поиск напряжённости поля.
Поле точечного заряда
Из определения напряжённости поля (3) следует, что точечный заряд q создаёт на расстоянии r от себя поле, напряжённость которого равна:
. (5)
Поле системы зарядов
Система точечных зарядов создаёт поле описываемое выражением (3). Однако заряд может быть распределён непрерывно в пространстве. В этом случае, для нахождения напряженности необходимо разбить систему зарядов на бесконечно малые части, написать вклад в суммарное поле 
, создаваемое произвольной частью этой системы с зарядом dq и, выполнив в (3) переход от суммирования к интегрированию, найти величину напряжённости. Заряд бесконечно малой части системы при этом надо записать в виде ρdV, σdS или λdl для объёмного, поверхностного или линейного распределения зарядов соответственно. Выражение для напряжённости электрического поля в случае объёмного распределения зарядов выглядит следующим образом:
, (6)
где 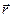– координата точки, где мы рассчитываем напряжённость, 
- координата объёма 
с плотностью заряда 
. Поскольку напряжённость - векторная величина, выражение (6) содержит три интеграла. То есть для нахождения, например, компоненты поля Ex, необходимо взять интеграл:
, (7)
где x и x’ – компоненты векторов 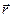и из формулы (6). Аналогичные (7) интегралы необходимо взять для нахождения Ey и Ez.
