1. Коэффициент корреляции 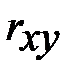 является безразмерной величиной и его значение не зависит от единиц измерения случайных величин Х и Y.
является безразмерной величиной и его значение не зависит от единиц измерения случайных величин Х и Y.
2. Абсолютная величина коэффициента корреляции 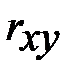 не превышает единицы: -1 ≤
не превышает единицы: -1 ≤ 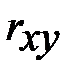 ≤ 1.
≤ 1.
3. Если 0< 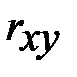 <1, то случайные величины Х и Y положительно коррелируемы, то есть с ростом одной величины вторая в среднем также растет (прямая корреляционная зависимость).
<1, то случайные величины Х и Y положительно коррелируемы, то есть с ростом одной величины вторая в среднем также растет (прямая корреляционная зависимость).
4. Если -1< 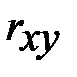 <0, то случайные величины Х и Y отрицательно коррелируемы, то есть с ростом одной величины вторая в среднем убывает (обратная корреляционная зависимость).
<0, то случайные величины Х и Y отрицательно коррелируемы, то есть с ростом одной величины вторая в среднем убывает (обратная корреляционная зависимость).
5. Если 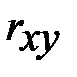 =0, то случайные величины Х и Y являются некоррелированными.
=0, то случайные величины Х и Y являются некоррелированными.
6. Если 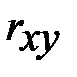 = ±1, то между случайными величинами Х и Y имеется точная линейная зависимость.
= ±1, то между случайными величинами Х и Y имеется точная линейная зависимость.
Качественная оценка корреляционной связи между случайными величинами может быть выявлена на основе шкалы Чеддока (табл. 10.1).
Т а б л и ц а 10.1
Значение
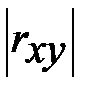
| 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Теснота связи | слабая | умеренная | заметная | высокая | очень высокая |
Практическая значимость коэффициента корреляции определяется его величиной, возведенной в квадрат, получившая название коэффициента детерминации.
Например, если 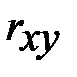 = 0,8, то
= 0,8, то 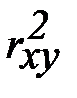 = 0,64, т.е. 64 % всех изменений одного признака связано с изменением другого.
= 0,64, т.е. 64 % всех изменений одного признака связано с изменением другого.
Доверительным интервалом статистической оценки истинного значения коэффициента корреляции нормально распределенных случайных величин Х и Y является интервал
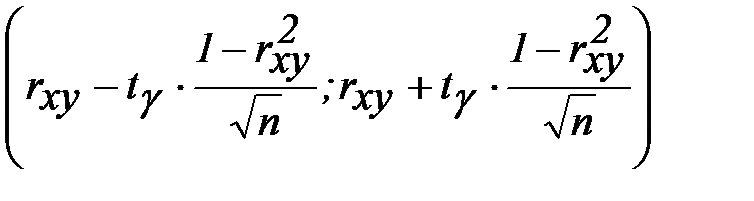 .
.
Здесь 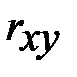 – выборочный коэффициент корреляции, величина
– выборочный коэффициент корреляции, величина 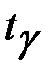 находится по таблице значений функции Лапласа (прил. 1) из условия Ф(
находится по таблице значений функции Лапласа (прил. 1) из условия Ф(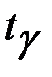 ) =
) = 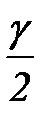 , где
, где 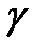 – заданный доверительный уровень.
– заданный доверительный уровень.
УРАВНЕНИЯ ЛИНЕЙНЫХ
СРЕДНЕКВАДРАТИЧЕСКИХ РЕГРЕССИЙ
Уравнением линейной среднеквадратической регрессии величины X на величину Y называется уравнение
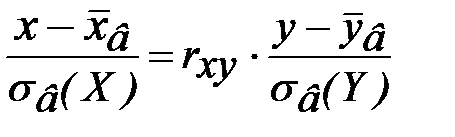 .
.
Уравнением линейной среднеквадратической регрессии величины Y на величину X называется уравнение
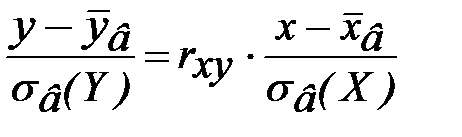 .
.
Пример 11.1
Найти коэффициент корреляции и составить уравнение линейной регрессии величины 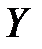 на величину
на величину 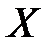 .
.
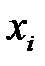
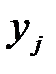
| 20 | 25 | 30 | 35 | 40 | 45 | 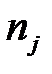
|
| 30 | 6 | 4 | 10 | ||||
| 40 | 4 | 1 | 5 | 7 | 17 | ||
| 50 | 3 | 4 | 5 | 6 | 18 | ||
| 60 | 5 | 3 | 10 | 2 | 20 | ||
| 70 | 2 | 3 | 3 | 5 | 13 | ||
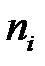
| 12 | 12 | 12 | 19 | 12 | 11 | 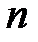 =78 =78
|
Решение.
Для упрощения расчетов введем условные варианты:
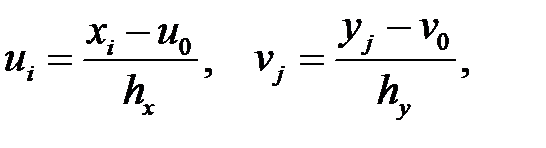
где 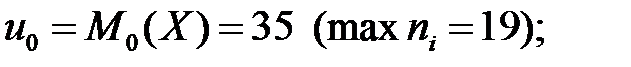
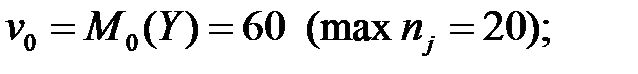
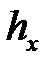 = 5 (разность между соседними значениями вариант
= 5 (разность между соседними значениями вариант 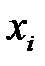 );
);
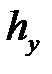 = 10 (разность между соседними значениями вариант
= 10 (разность между соседними значениями вариант 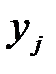 ).
).
Составим корреляционную таблицу с условными вариантами:
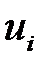
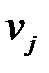
| –3 | –2 | –1 | 0 | 1 | 2 | 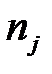
|
| –3 | 6 | 4 | 10 | ||||
| –2 | 4 | 1 | 5 | 7 | 17 | ||
| –1 | 3 | 4 | 5 | 6 | 18 | ||
| 0 | 5 | 3 | 10 | 2 | 20 | ||
| 1 | 2 | 3 | 3 | 5 | 13 | ||
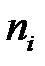
| 12 | 12 | 12 | 19 | 12 | 11 | 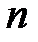 =78 =78
|
Затем находим 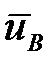 и
и 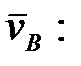
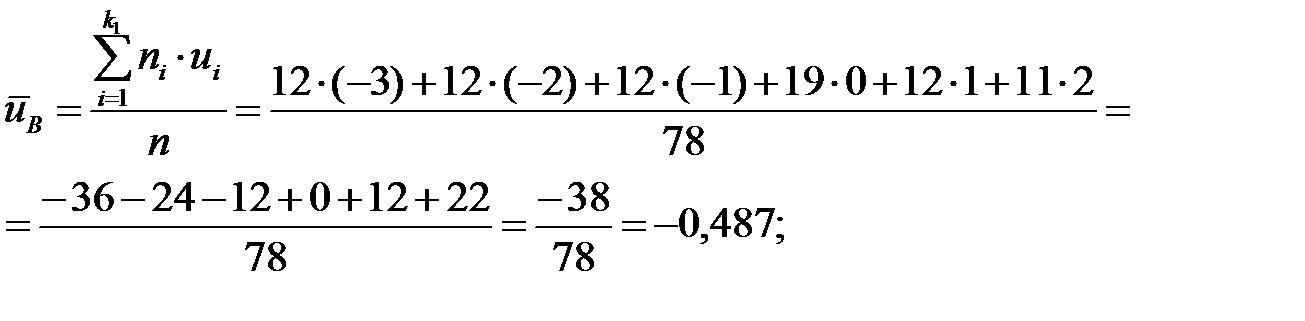
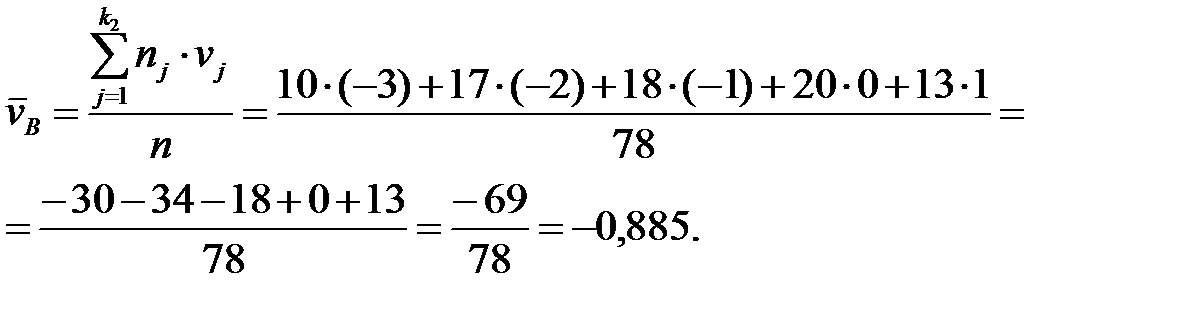
Теперь находим 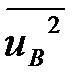 и
и 
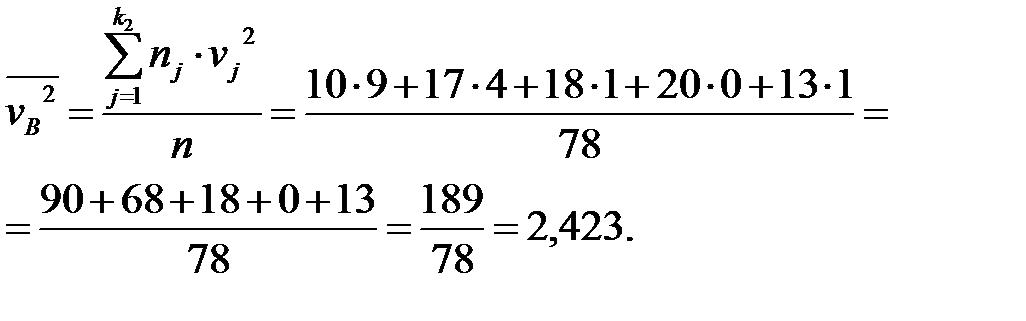
Определяем 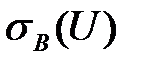 и
и 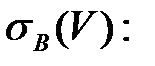
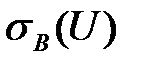 =
= 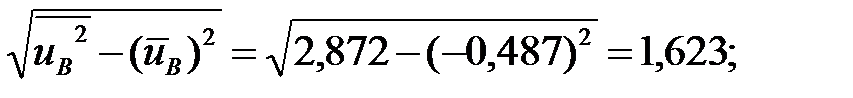
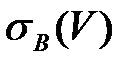 =
= 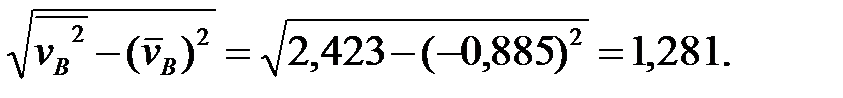
Коэффициент корреляции 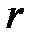 найдем по формуле
найдем по формуле
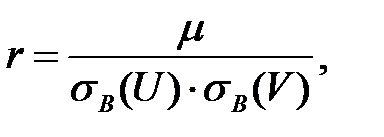
где 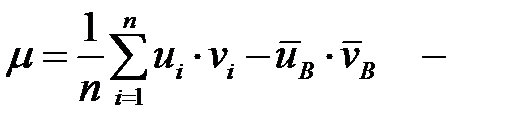 корреляционный момент.
корреляционный момент.
При вычислении 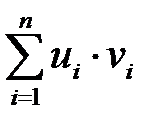 складываем члены вида
складываем члены вида 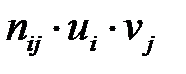 (
(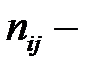 частота появления пары (
частота появления пары (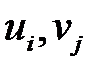 )):
)):
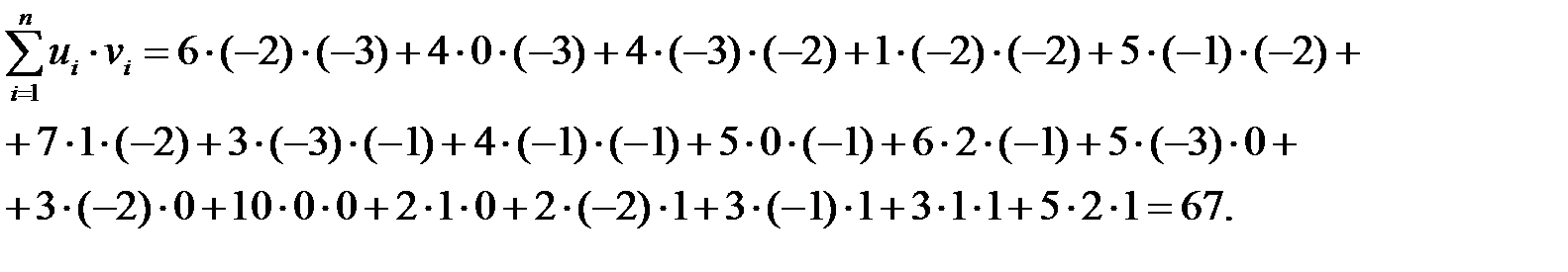
Тогда 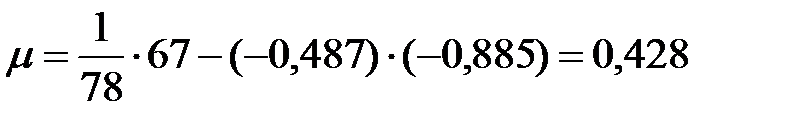 , а значит
, а значит
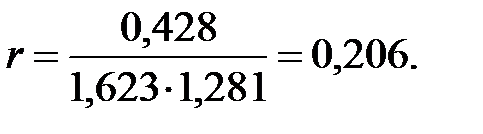
Осуществим переход к исходным вариантам:
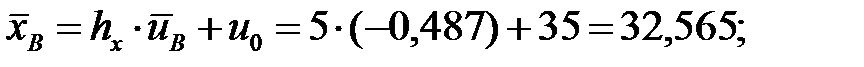
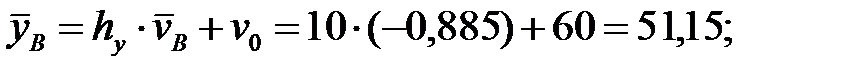
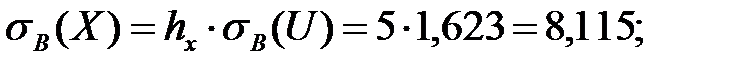
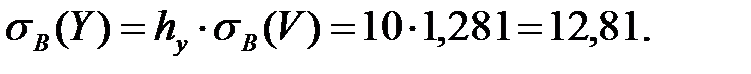
Находим уравнение линейной регрессии величины  на величину
на величину  . Это уравнение имеет вид:
. Это уравнение имеет вид:
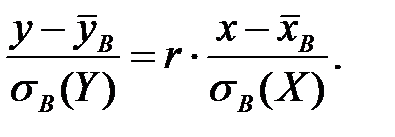
Подставляя вычисленные значения 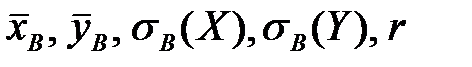 в это уравнение, получаем
в это уравнение, получаем
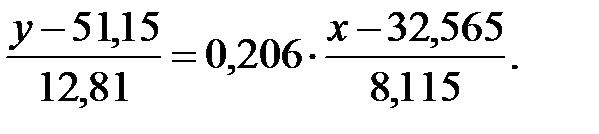
После упрощения получаем уравнение линейной регрессии величины 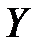 на величину
на величину 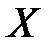 в виде:
в виде:
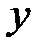 =0,325
=0,325 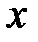 +40,566.
+40,566.
 2020-09-24
2020-09-24 92
92








