Случайной величиной называется величина, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Приведем некоторые примеры случайных величин.
1) Число очков, выпадающих на игральной кости. Эта величина может принимать одно из следующих значений: 1, 2, 3, 4, 5, 6.
2) Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, …, 100.
3) Расстояние, которое пролетит снаряд при выстреле из орудия. Возможные значения этой величины принадлежат некоторому промежутку (а, b).
Случайные величины в дальнейшем будем обозначать большими буквами X, Y, Z а их возможные значения – соответственно строчными буквами x, y, z. Например, X – число попаданий при трех выстрелах. Возможные значения этой случайной величины: x1 = 0, x2 =1, x3 =2, x4 =3.
Случайная величина называется дискретной, если её возможные значения есть отдельные изолированные числа (т. е. между двумя соседними возможными значениями нет других значений). Дискретная случайная величина принимает эти значения с определенными вероятностями.
Из приведенных выше случайных величин дискретными являются случайные величины примеров 1, 2.
Бывают случайные величины, которые принимают значения из некоторого интервала.
К таким величинам относится случайная величина примера 3.
Чтобы охарактеризовать дискретную случайную величину X, следует указать её возможные значения x1, x2, …, xn и вероятности событий, состоящих в том, что случайная величина X приняла значение xi:
pi = P(X = xi), (i =1, 2, …, n).
В результате испытания произойдет только одно из полной группы событий: X=x1, X=x2, …, X=xn. Поскольку сумма вероятностей полной группы попарно несовместных событий равна 1, то 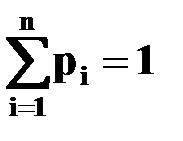 .
.
Законом распределения дискретной случайной величины называют соответствие между возможными её значениями и их вероятностями.
Для дискретной случайной величины закон распределения удобно записывать в виде таблицы, первая строка которой содержит возможные значения xi, а вторая – их вероятности pi:
| X | x1 | x2 | … | xn |
| P | p1 | p2 | … | pn |
Эта таблица называется рядом распределения.
Пусть x – некоторое действительное число. Вероятность события, состоящего в том, что X примет значение меньше x, обозначим через F(x), т. е. 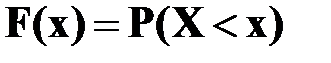 .
.
Функция F(x) называется функцией распределения случайной величины X.
Случайная величина называется непрерывной, если её функция распределения непрерывна и кусочно-дифференцируема.
Функция распределения обладает следующими свойствами:
1. Значения функции распределения принадлежат отрезку [0; 1]:
0 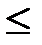 F(x)
F(x) 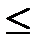 1.
1.
2. Функция распределения есть неубывающая функция:
F(x2) 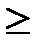 F(x1), если x2 >x1.
F(x1), если x2 >x1.
3. Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), равна приращению функции распределения на этом интервале:
P (a < X < b) = F (b) – F (a).
4. Справедливы следующие предельные соотношения:
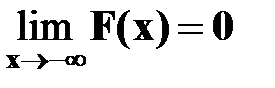 ,
, 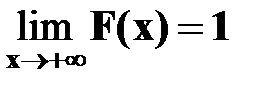 .
.
Плотностью распределения вероятностей непрерывной случайной величины Х называют первую производную от функции распределения:
f(x) = 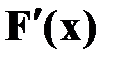 .
.
Зная плотность распределения f(x), можно найти функцию распределения F(x) по формуле
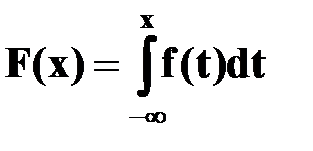 .
.
Свойства плотности распределения:
1. Плотность распределения неотрицательна, т. е.
f(x) 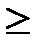 0.
0.
2. Несобственный интеграл от плотности распределения в пределах от – ∞ до ∞ равен единице:
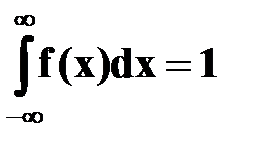 .
.
3. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a, b), определяется равенством
P (a < X < b) = 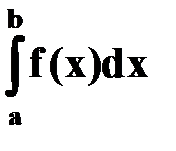 .
.
Для решения многих практических задач совсем необязательно знать все возможные значения случайной величины и соответствующие им вероятности, а достаточно указать отдельные числовые параметры, которые позволяют отразить существенные особенности случайной величины.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на соответствующие им вероятности: M(X) =x1 p1+x2 p2+…+xn pn.
Математическое ожидание непрерывной случайной величины, возможные значения которой принадлежат всей оси Ox, определяется равенством
M(X) = 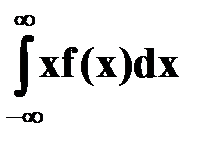 .
.
Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой постоянной:
M (С) = С.
2. Постоянный множитель можно выносить за знак математического ожидания:
M (CX) = CM(X).
3. Математическое ожидание суммы (разности) двух случайных величин равно сумме (разности) математических ожиданий этих величин:
M(X 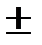 Y) = M(X)
Y) = M(X) 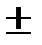 M (Y).
M (Y).
4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M (X∙Y) = M(X) ∙ M(Y).
Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
D(X) =M(X – M(X))2.
Дисперсию удобно вычислять по формуле
D(X) =M(X2) – (M(X)) 2.
Если X является дискретной случайной величиной, то
D(X) = 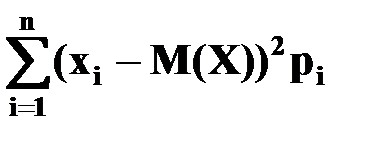
или D(X) = 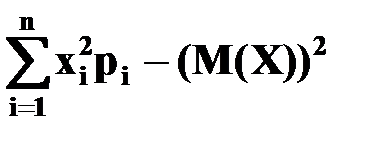 .
.
Для непрерывной случайной величины
D(X) = 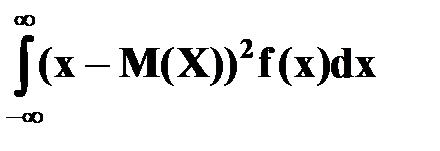 или D(X) =
или D(X) = 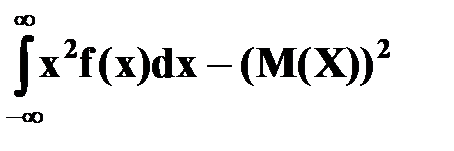 .
.
Дисперсия обладает следующими свойствами:
1. Дисперсия постоянной величины равна нулю:
D (С) =0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
D (CX) =C2D(X).
3. Дисперсия суммы или разности двух независимых случайных величин равна сумме их дисперсий:
D(X ± Y) = D(X) + D(Y).
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии: 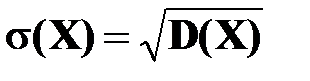 .
.
7. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Пример 7.1. Независимые испытания производятся до тех пор, пока не появится событие А. Вероятность появления события А в каждом испытании 0,7. Максимальное число испытаний – 3. Составить ряд распределения числа произведенных испытаний. Найти числовые характеристики этой случайной величины. Какова вероятность, что произойдет не более двух испытаний?
Решение. Случайная величина X – число произведенных испытаний – может принимать следующие значения: x1=1, x2=2, x3=3.
Случайная величина X примет значение x1=1, когда событие А произойдет в первом испытании.
P(X=1) =P (A) =0,7.
Случайная величина X примет значение x2=2, если событие А не произойдет в первом испытании, но произойдет во втором.
P(X=2) =P (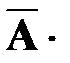 A) =
A) = 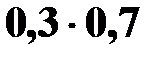 =0,21.
=0,21.
Случайная величина X примет значение x3=3, если событие А не появится ни при первом, ни при втором испытании. Так как число испытаний не более трех, то не важно произойдет событие А в третьем испытании или нет.
P(X=3) =P (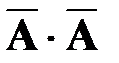 ) =
) = 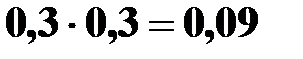 .
.
Составим ряд распределения случайной величины X.
| X | 1 | 2 | 3 |
| P | 0,7 | 0,21 | 0,09 |
Проверим тождество 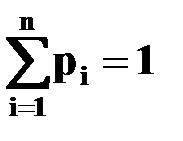 . Действительно, 0,7+0,21+0,09=1.
. Действительно, 0,7+0,21+0,09=1.
Найдем числовые характеристики случайной величины X.
M(X) = 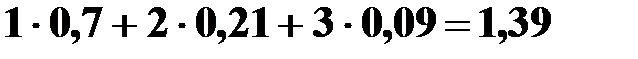 .
.
Для вычисления дисперсии применим формулу
D(X) =M(X2) – (M(X)) 2.
Составим ряд распределения случайной величины X2:
| X2 | 1 | 4 | 9 |
| P | 0,7 | 0,21 | 0,09 |
Найдем математическое ожидание случайной величины X2:
M(X2) = 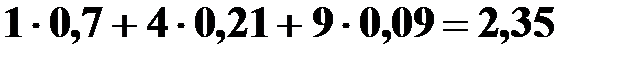 .
.
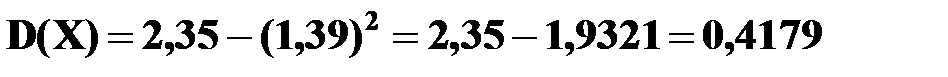 .
.
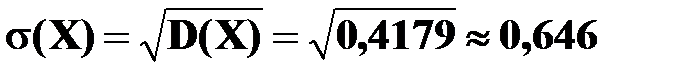 .
.
Пусть событие В – произойдет не более двух испытаний, т. е. произойдет или одно, или два испытания.
P(B)=P(X=1)+P(X=2)=0,7+0,21=0,91.
 2020-09-24
2020-09-24 211
211








