2020-09-24
68
Пример 8.1. Случайная величина Х задана функцией распределения
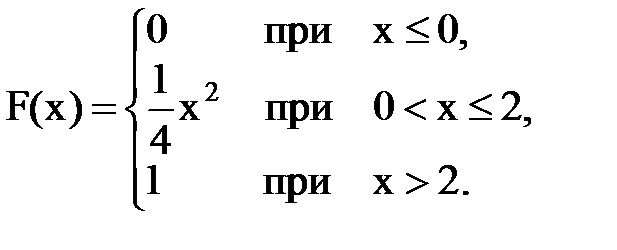
Найти:
1) вероятность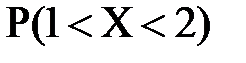 
;
2) плотность вероятности f(x);
3) математическое ожидание M(X) и дисперсию D(X).
Решение.
1) Воспользуемся формулой P (a < X < b) = F (b) – F (a). По условию a=1, b=2. Следовательно, искомая вероятность
.
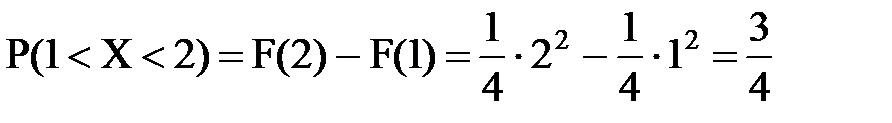2) Плотность распределения равна первой производной от функции распределения:
f(x) =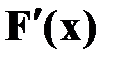 
= 
4) Вычислим числовые характеристики случайной величины Х.
Математическое ожидание
M(X) =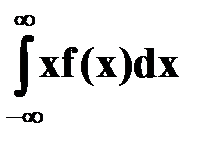 
= 
.
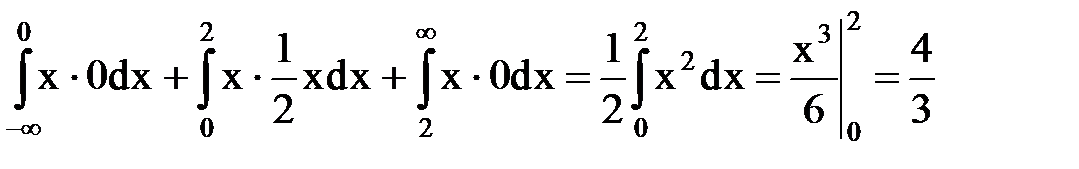Дисперсия
D(X)=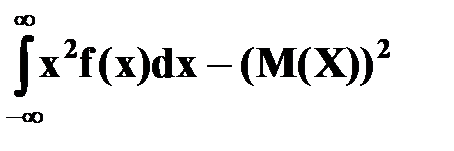 
= 
.
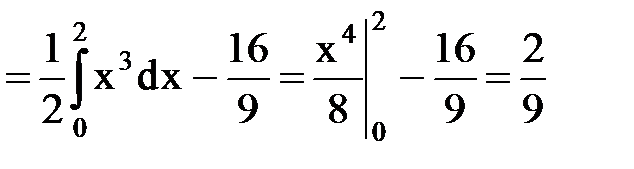НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
Непрерывная случайная величина Х распределена по нормальному закону, если её плотность распределения вероятностей задается функцией
,
где 
– математическое ожидание,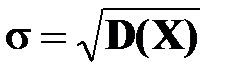 
– среднее квадратическое отклонение.
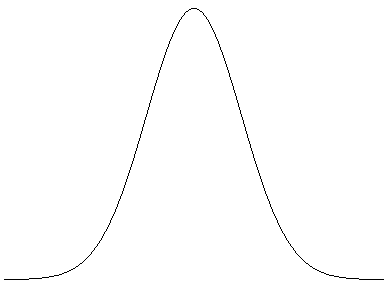
График функции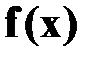 
называют нормальной кривой или кривой Гаусса.
Вероятность того, что случайная величина Х примет значение, принадлежащее интервалу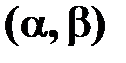 
, равна
,
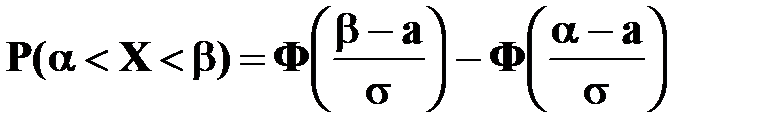где
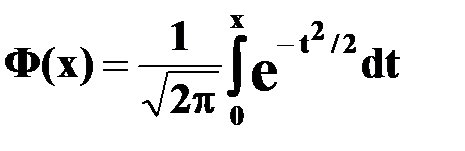– функция Лапласа. 
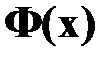– функция нечетная, т. е. 
.
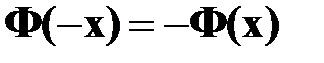f(x)
a x
Вероятность того, что абсолютная величина отклонения нормально распределенной случайной величины Х от своего математического ожидания будет меньше положительного числа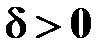 
, равна
.
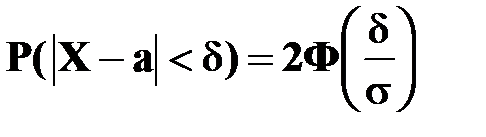Пример 9.1. Математическое ожидание нормально распределенной случайной величины Х равно М(Х)=8 и дисперсия D(X)=9. Написать плотность вероятности Х. Найти вероятность того, что Х примет значение из интервала (1, 6).
Решение. Так как случайная величина Х имеет нормальное распределение, то её плотность имеет вид:
,
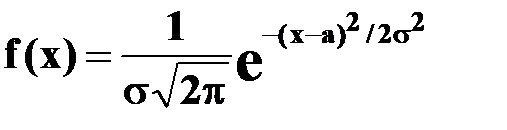где = 8, =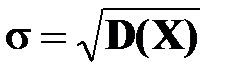 
.
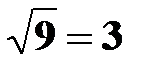Тогда
.
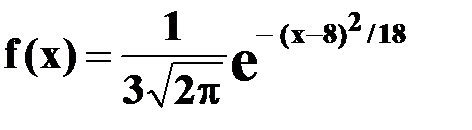Вычислим вероятность того, что случайная величина Х будет принимать значения из интервала (1, 6):
.
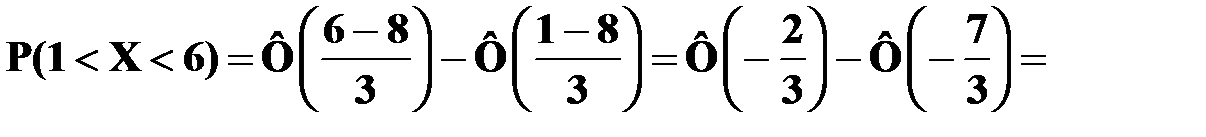
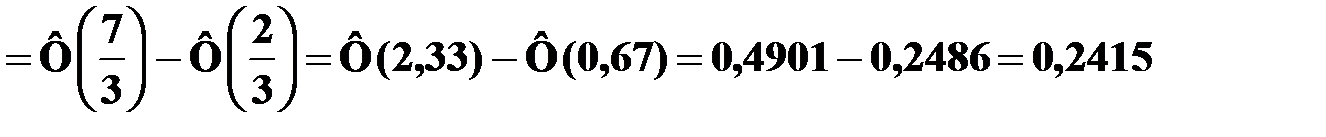ВЫБОРОЧНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Пусть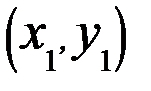 
, 
, 
, …, 
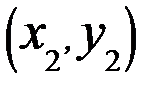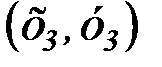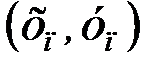выборка объема n для двух случайных величин Х и Y.
Выборочным коэффициентом корреляции называется величина
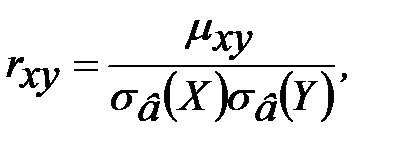
где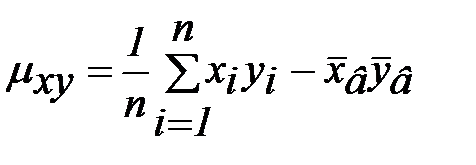 
– выборочный корреляционный момент,
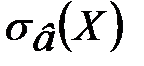и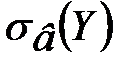 
– выборочные средние квадратические отклонения
случайных величин X и Y соответственно.
Коэффициент корреляции представляет собой меру линейной зависимости случайными величинами X и Y.
