Если известно, что событие 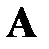 может произойти только совместно с одним из событий (гипотез)
может произойти только совместно с одним из событий (гипотез) 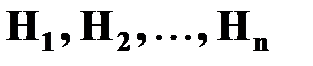 , которые образуют полную группу попарно несовместных событий, то вероятность события
, которые образуют полную группу попарно несовместных событий, то вероятность события 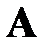 вычисляется по формуле полной вероятности
вычисляется по формуле полной вероятности
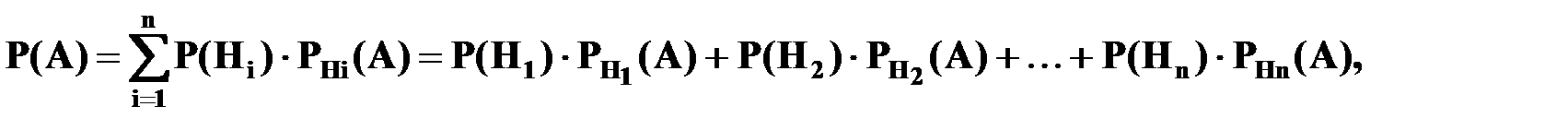 где
где 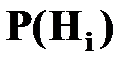 - вероятность гипотезы
- вероятность гипотезы 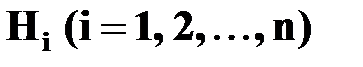 ,
,
причем 
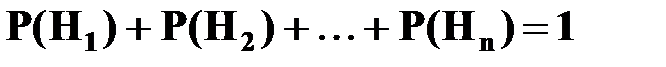 ;
;
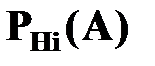 - условная вероятность события
- условная вероятность события  , т.е. вероятность события при условии, что произошла гипотеза
, т.е. вероятность события при условии, что произошла гипотеза 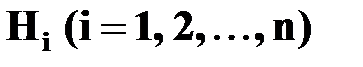 .
.
Для определения вероятности гипотезы 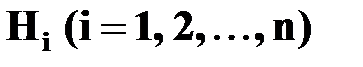 при условии, что в результате опыта произошло событие
при условии, что в результате опыта произошло событие  , используется формула Бейеса
, используется формула Бейеса
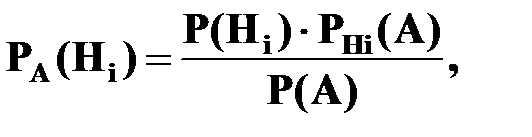
где  формула полной вероятности.
формула полной вероятности.
Формула Бейеса позволяет переоценить вероятности гипотез, принятых до опыта, после того, как становится известным результат испытания, в итоге которого появилось событие 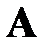 .
.
Пример 4.1 Два автомата изготавливают одинаковые детали. Известно, что первый автомат производит 30% всей продукции. Вероятность изготовления детали, соответствующей стандарту, первым автоматом равна 0,99, вторым – 0,98. Все изготовленные за смену детали складываются вместе. Определите вероятность того, что взятая наудачу деталь не соответствует стандарту.
Решение. Пусть событие 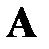 - взятая наудачу деталь не соответствует стандарту.
- взятая наудачу деталь не соответствует стандарту.
Гипотезы:
 - взятая деталь изготовлена первым автоматом;
- взятая деталь изготовлена первым автоматом;
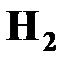 - взятая деталь изготовлена вторым автоматом.
- взятая деталь изготовлена вторым автоматом.
События 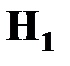 ,
,  - несовместны и образуют полную группу.
- несовместны и образуют полную группу.
Вычислим вероятности гипотез.

Вычислим условные вероятности:
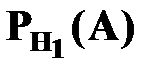 - вероятность изготовления детали не соответствующей стандарту первым автоматом;
- вероятность изготовления детали не соответствующей стандарту первым автоматом;
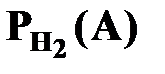 - вероятность изготовления детали не соответствующей стандарту вторым автоматом.
- вероятность изготовления детали не соответствующей стандарту вторым автоматом.

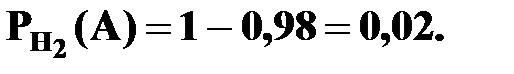
Вероятность события 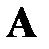 находим по формуле полной вероятности:
находим по формуле полной вероятности:
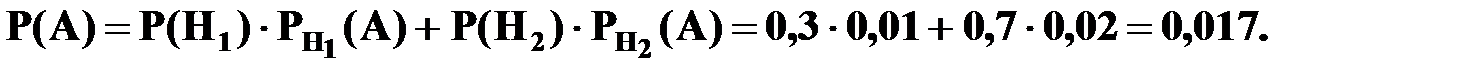
ФОРМУЛА БЕРНУЛЛИ
Пусть производится 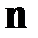 независимых однотипных испытаний, в каждом из которых событие
независимых однотипных испытаний, в каждом из которых событие  может появиться с вероятностью
может появиться с вероятностью  . Тогда вероятность непоявления события
. Тогда вероятность непоявления события  , т.е.
, т.е.  , равна
, равна  .
.
Вероятность того, что событие  произойдет в этих
произойдет в этих 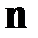 независимых испытаниях ровно
независимых испытаниях ровно 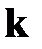 раз (безразлично в какой последовательности), можно вычислить по формуле Бернулли
раз (безразлично в какой последовательности), можно вычислить по формуле Бернулли
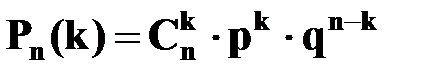 .
.
Вероятность того, что в 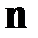 испытаниях событие наступит:
испытаниях событие наступит:
а) менее 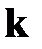 раз:
раз: 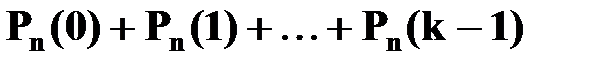 ;
;
б) более 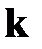 раз:
раз:  ;
;
в) не менее 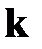 раз:
раз: 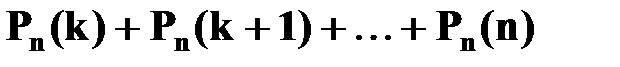 ;
;
г) не более 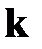 раз:
раз: 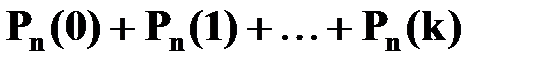 .
.
Пример 5.1. Вероятность выигрыша по одному лотерейному билету равна 1/5. Вы купили 5 билетов. Найти вероятность того, что а) четыре билета выигрышные; б) хотя бы один билет выигрышный; в) более трех билетов выигрышные.
Решение. Пусть событие  - выигрыш по лотерейному билету. Число лотерейных билетов
- выигрыш по лотерейному билету. Число лотерейных билетов 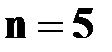 .
.  - вероятность выигрыша по лотерейному билету:
- вероятность выигрыша по лотерейному билету:  Тогда
Тогда 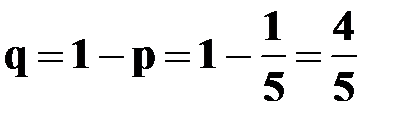 .
.
а) Вероятность того, что выигрышными будут четыре билета ( )
)
 .
.
б) Пусть событие В – хотя бы один из купленных билетов выигрышный. Рассмотрим событие  , противоположное событию В:
, противоположное событию В:
 - среди купленных билетов нет выигрышных.
- среди купленных билетов нет выигрышных.
P (  ) =
) = 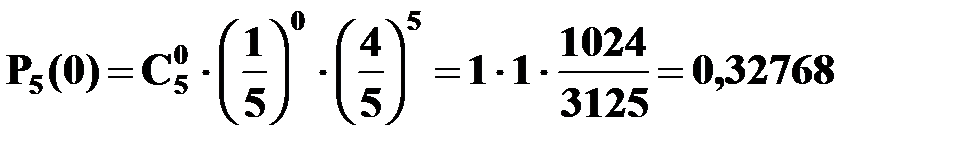 .
.
Теперь вычислим вероятность искомого события:
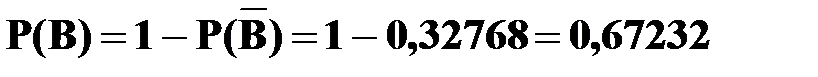 .
.
в) Вероятность того, что выигрышными будут более трех билетов (т.е. или четыре, или пять)
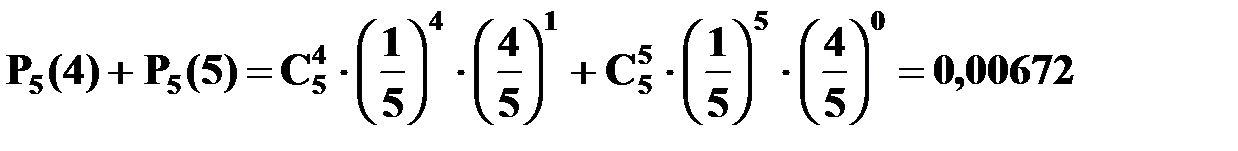 .
.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
 2020-09-24
2020-09-24 82
82








