2020-09-24
212
| t |
|
| 55 | 0,110803 |
| 56 | 0,106459 |
| 57 | 0,102284 |
| 58 | 0,098274 |
| 59 | 0,09442 |
| 60 | 0,090718 |
| 61 | 0,087161 |
| 62 | 0,083743 |
| 63 | 0,08046 |
| 64 | 0,077305 |
| 65 | 0,074274 |
| 66 | 0,071361 |
| 67 | 0,068563 |
| 68 | 0,065875 |
| 69 | 0,063292 |
| 70 | 0,06081 |
| 71 | 0,058426 |
| 72 | 0,056135 |
| 73 | 0,053934 |
| 74 | 0,051819 |
| 75 | 0,049787 |
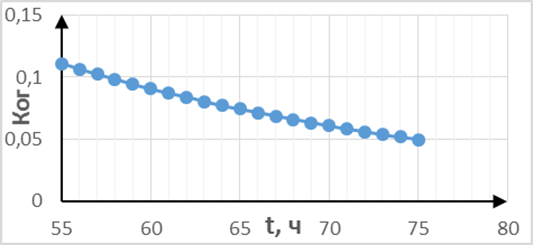
Рисунок 7 – График функции оперативной готовности на интервале
(от t до t +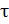 
)
Найдем зависимость коэффициента готовности для 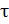(от 0 до 100 ч):
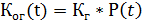
Вычислив значения построим график (рисунок 8)
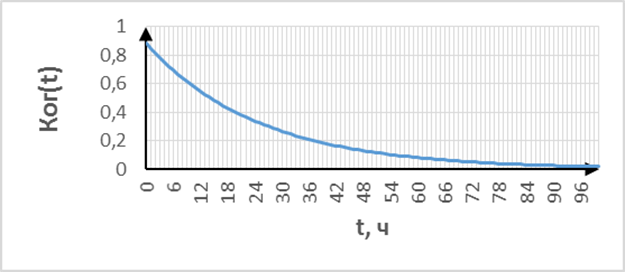
Рисунок 8 – зависимость коэффициента готовности для t
(от 0 до 100 ч)
Вывод:
В данной задаче по исходным данным были найдены среднее время безотказной работы и среднее время восстановления равные 25 часов и 3,33 часа соответственно, коэффициент готовности равный 0,88 и были построены графики функции оперативной готовности, функции готовности.
Затраченное время: 4 часа.
Общий вывод:
В данной лабораторной работе были решены 3 задания с целью получения навыков в расчёте показателей надёжности восстанавливаемых и невосстанавливаемых технических систем.
Процесс вычисления данных параметров был автоматизирован в программе MS Exсel.
