2020-09-24
295
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
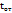
| 354 | 372 | 320 | 330 | 300 | 310 | 300 | 290 | 295 | 270 | 240 | 260 | 250 | 200 | 210 | 180 | 160 | 190 | 170 | 130 |
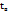
| 12 | 14 | 14 | 20 | 18 | 16 | 15 | 15 | 16 | 20 | 20 | 18 | 17 | 15 | 17 | 19 | 15 | 19 | 20 | 14 |
Средняя наработка на отказ определяется по формуле:
,
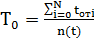где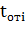 
- наработка между i-1 и i-м отказами; n(t) - суммарное число отказов за время t.
Найдем среднюю наработку на отказ:
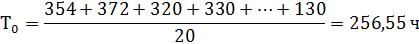
Среднее время восстановления найдем по формуле:
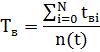
Подставляя значения, получим:
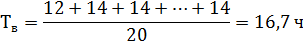
Коэффициент готовности определяется по формуле:
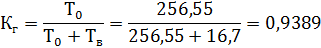
Найдем параметр потока отказов по формуле:
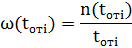
где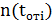 
- количество отказов объекта, зафиксированных соответственно, по истечении времени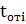 
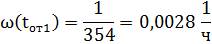
Далее аналогично находим оставшиеся значения:
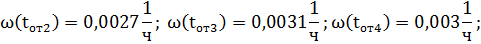
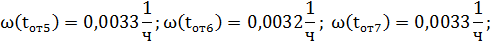
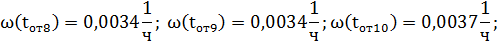
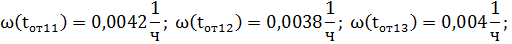
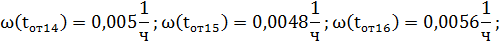
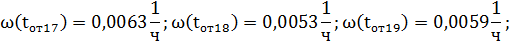
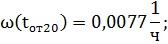
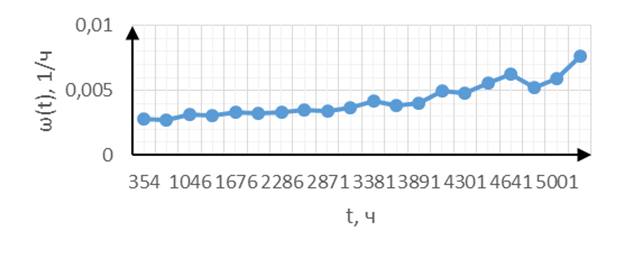График функции потока параметра отказов представлен на рисунке 3.
Рисунок 4 
- График функции потока параметра отказов
Определим функциональную зависимость параметра потока отказов от наработки с интервалом в 1000 ч:
Для этого найдем количество отказов за все время наработки (0 - 8290). Данные сведены в таблицу 1.3
Таб. 1.3 – Количество отказов за время наработки
| t | № отказа |
| 354 | 1 |
| 726 | 2 |
| 1046 | 1 |
| 1376 | 2 |
| 1676 | 3 |
| 1986 | 4 |
| 2286 | 1 |
| 2576 | 2 |
| 2871 | 3 |
| 3141 | 1 |
| 3381 | 2 |
| 3641 | 3 |
| 3891 | 4 |
| 4091 | 1 |
| 4301 | 2 |
| 4481 | 3 |
| 4641 | 4 |
| 4831 | 5 |
| 5001 | 1 |
| 5131 | 2 |
За интервал от 0 до 1000 ч произошло 2 отказа, за интервал от 1000 до 2000 произошло 4 отказа.
Оставшиеся данные сведены в таблицу 1.4
Таб. 1.4 – Функциональная зависимость параметра потока отказов от наработки
|
| 2 | 4 | 3 | 4 | 5 | 2 |
| ∆t | 0-1000 | 1000-2000 | 2000-3000 | 3000-4000 | 4000-5000 | 5000-6000 |
| ω(t) | 0,002 | 0,004 | 0,003 | 0,004 | 0,005 | 0,002 |
Вывод: В данной задаче мы определили среднюю наработку на отказ равную Tо = 256,55 ч, среднее время восстановления Тв = 16,7ч, коэффициент готовности Кг = 0,9389. Также определили функциональную зависимость параметра потока отказов от наработки и построили график функции ω(t).
По графику можно сказать, что параметр потока отказов растёт, что соответствует 3 периоду — старению и износу объектов.
Затраченное время: 3 часа.
Задание 1.3.
Восстанавливаемый объект имеет постоянные интенсивности отказов и восстановлений. Исходные данные представлены в таблице 1.5. Предполагается, что справедлив экспоненциальный закон надежности. Требуется найти: параметр потока отказов, среднее время безотказной работы (среднюю наработку на отказ), среднее время восстановления, функцию готовности (от 0 до t), коэффициент готовности, функцию оперативной готовности для времени (от 0 до τ), интервал оперативной готовности (от t до t + τ), зависимость коэффициента готовности для τ (от 0 до 100 ч).
