УРАВНЕНИЕ ЛИНЕЙНОЙ РЕГРЕССИИ
Практическая часть
Пример 8.1. Найти коэффициент корреляции и составить уравнение линейной регрессии величины 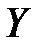 на величину
на величину 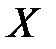 .
.


| 20 | 25 | 30 | 35 | 40 | 45 | 
|
| 30 | 6 | 4 | 10 | ||||
| 40 | 4 | 1 | 5 | 7 | 17 | ||
| 50 | 3 | 4 | 5 | 6 | 18 | ||
| 60 | 5 | 3 | 10 | 2 | 20 | ||
| 70 | 2 | 3 | 3 | 5 | 13 | ||

| 12 | 12 | 12 | 19 | 12 | 11 |  =78 =78
|
Решение.
Для упрощения расчетов введем условные варианты:
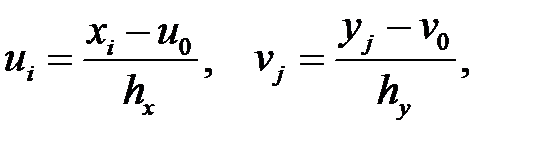
где 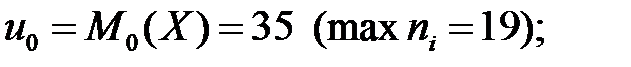
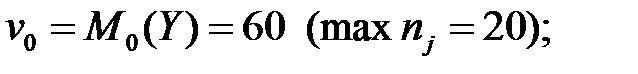
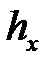 = 5 (разность между соседними значениями вариант
= 5 (разность между соседними значениями вариант  );
);
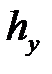 = 10 (разность между соседними значениями вариант
= 10 (разность между соседними значениями вариант  ).
).
Составим корреляционную таблицу с условными вариантами:
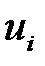
| –3 | –2 | –1 | 0 | 1 | 2 | 
|
| –3 | 6 | 4 | 10 | ||||
| –2 | 4 | 1 | 5 | 7 | 17 | ||
| –1 | 3 | 4 | 5 | 6 | 18 | ||
| 0 | 5 | 3 | 10 | 2 | 20 | ||
| 1 | 2 | 3 | 3 | 5 | 13 | ||

| 12 | 12 | 12 | 19 | 12 | 11 |  =78 =78
|
Затем находим 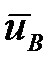 и
и 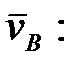
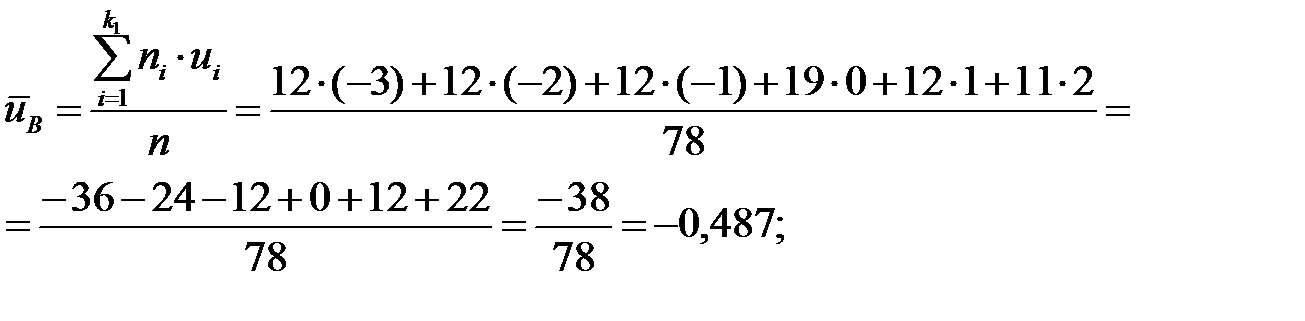
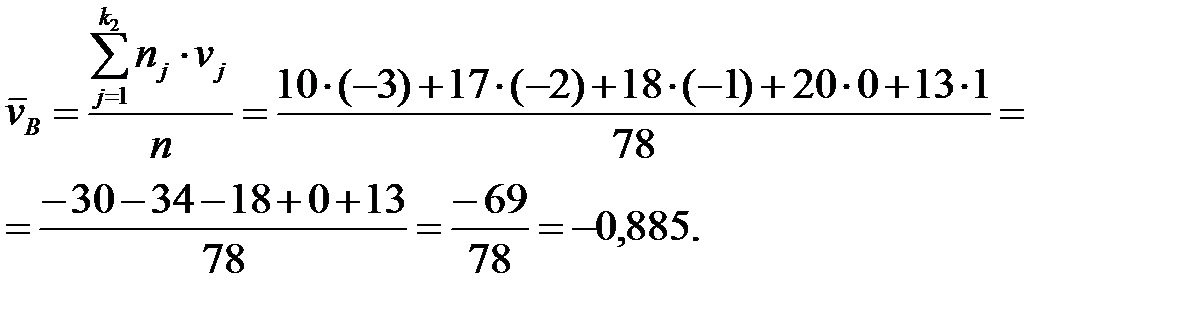
Теперь находим 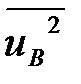 и
и 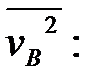
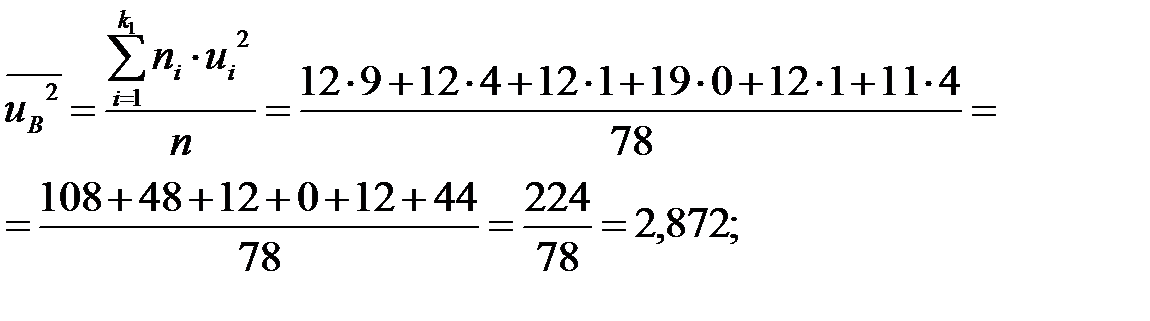
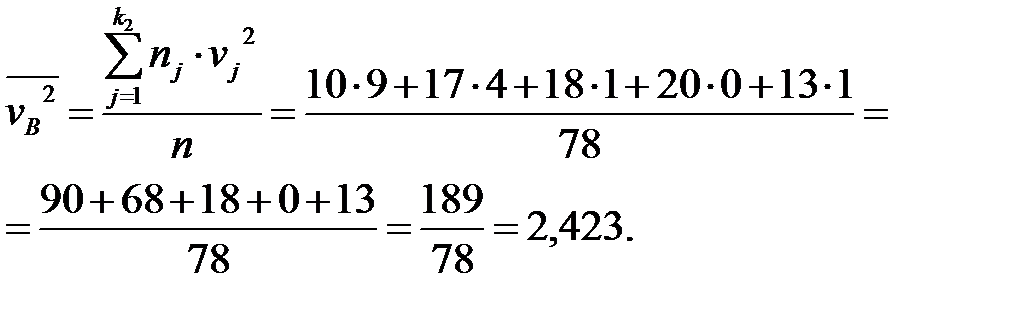
Определяем 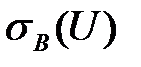 и
и 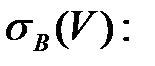
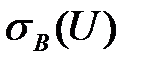 =
= 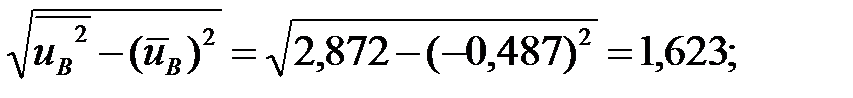
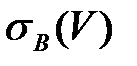 =
= 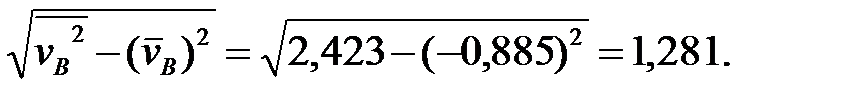
Коэффициент корреляции 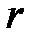 найдем по формуле
найдем по формуле
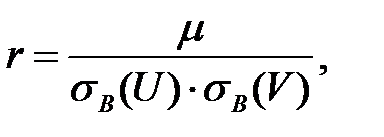
где 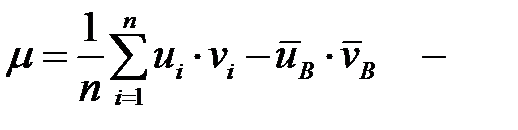 корреляционный момент.
корреляционный момент.
При вычислении 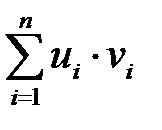 складываем члены вида
складываем члены вида 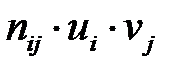 (
(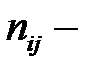 частота появления пары (
частота появления пары (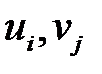 )):
)):
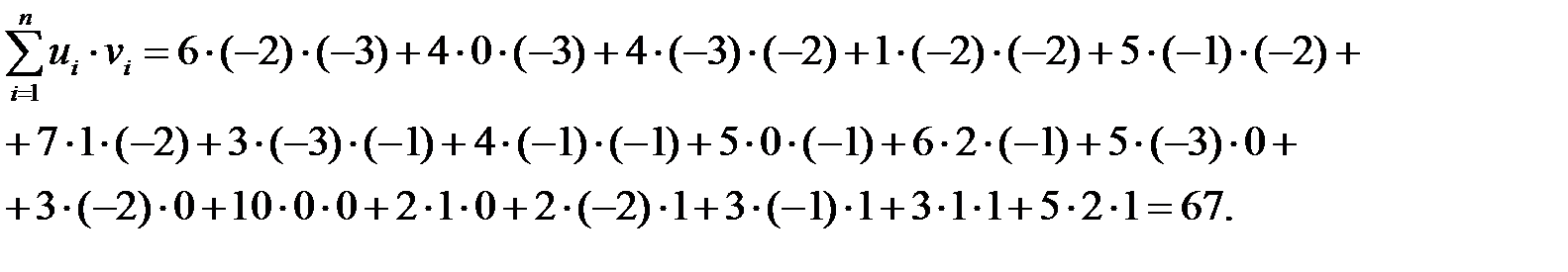
Тогда 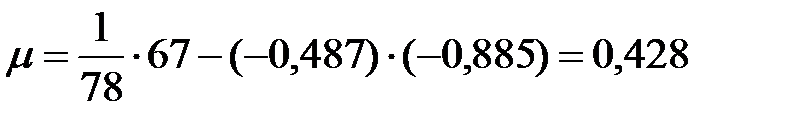 , а значит
, а значит
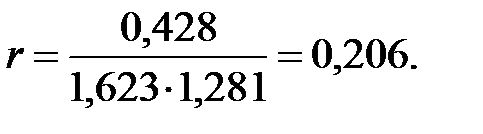
Осуществим переход к исходным вариантам:
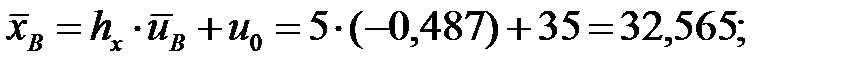
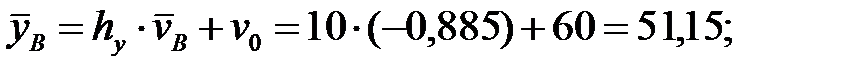
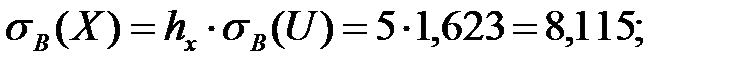
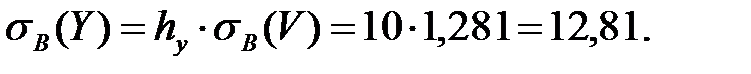
Находим уравнение линейной регрессии величины 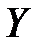 на величину
на величину 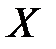 . Это уравнение имеет вид:
. Это уравнение имеет вид:
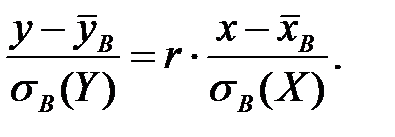
Подставляя вычисленные значения 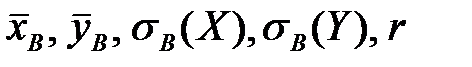 в это уравнение, получаем
в это уравнение, получаем
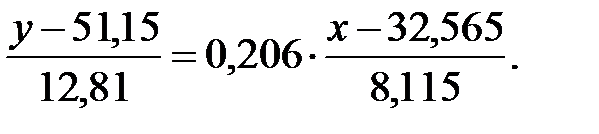
После упрощения получаем уравнение линейной регрессии величины 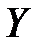 на величину
на величину 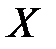 в виде:
в виде:
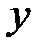 =0,325
=0,325 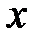 +40,566.
+40,566.
Индивидуальные задания
Найти коэффициент корреляции и составить уравнение линейной регрессии величины 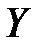 на величину
на величину 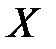 .
.
Вариант 1


| 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 15 | 6 | 4 | 10 | ||||
| 25 | 6 | 8 | 14 | ||||
| 35 | 21 | 2 | 5 | 28 | |||
| 45 | 4 | 12 | 6 | 22 | |||
| 55 | 1 | 5 | 6 | ||||

| 6 | 10 | 8 | 25 | 15 | 16 |  =80 =80
|
Вариант 2


| 20 | 25 | 30 | 35 | 40 | 45 | 
|
| 10 | 4 | 8 | 4 | 16 | |||
| 20 | 2 | 4 | 2 | 8 | |||
| 30 | 10 | 8 | 18 | ||||
| 40 | 4 | 10 | 4 | 18 | |||

| 2 | 8 | 22 | 18 | 6 | 4 |  =60 =60
|
Вариант 3


| 5 | 10 | 15 | 20 | 25 | 30 | 
|
| 14 | 4 | 6 | 8 | 4 | 22 | ||
| 24 | 8 | 10 | 6 | 24 | |||
| 34 | 32 | 32 | |||||
| 44 | 4 | 12 | 6 | 22 | |||

| 4 | 14 | 46 | 20 | 12 | 4 |  =100 =100
|
Вариант 4


| 15 | 20 | 25 | 30 | 35 | 40 | 
|
| 100 | 2 | 1 | 7 | 10 | |||
| 120 | 4 | 2 | 3 | 9 | |||
| 140 | 5 | 10 | 5 | 2 | 22 | ||
| 160 | 3 | 1 | 2 | 3 | 9 | ||

| 6 | 6 | 5 | 18 | 7 | 8 |  =50 =50
|
Вариант 5


| 12 | 17 | 22 | 27 | 32 | 37 | 
|
| 105 | 4 | 3 | 7 | ||||
| 115 | 2 | 3 | 1 | 10 | 16 | ||
| 125 | 3 | 5 | 1 | 4 | 13 | ||
| 135 | 8 | 2 | 1 | 11 | |||
| 145 | 1 | 2 | 3 | ||||

| 6 | 9 | 6 | 12 | 12 | 5 |  =50 =50
|
Вариант 6


| 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 14 | 4 | 2 | 1 | 7 | |||
| 24 | 2 | 1 | 3 | 8 | 5 | 19 | |
| 34 | 4 | 2 | 1 | 3 | 10 | ||
| 44 | 3 | 2 | 10 | 3 | 2 | 20 | |
| 54 | 1 | 3 | 9 | 1 | 14 | ||

| 6 | 10 | 16 | 15 | 12 | 11 |  =70 =70
|
Вариант 7


| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 5 | 10 | 3 | 5 | 1 | 4 | 23 | ||
| 15 | 4 | 10 | 2 | 8 | 24 | |||
| 25 | 3 | 4 | 6 | 6 | 19 | |||
| 35 | 4 | 7 | 1 | 5 | 17 | |||
| 45 | 2 | 5 | 10 | 17 | ||||

| 15 | 13 | 13 | 15 | 19 | 10 | 15 |  =100 =100
|
Вариант 8

 j j
| 24 | 28 | 32 | 36 | 40 | 44 | 48 | 
|
| 10 | 6 | 4 | 2 | 5 | 17 | |||
| 20 | 4 | 5 | 7 | 1 | 17 | |||
| 30 | 4 | 3 | 5 | 6 | 18 | |||
| 40 | 5 | 3 | 10 | 2 | 20 | |||
| 50 | 4 | 10 | 4 | 2 | 8 | 28 | ||

| 9 | 13 | 12 | 19 | 21 | 7 | 19 |  =100 =100
|
Вариант 9


| 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 36 | 4 | 3 | 7 | ||||
| 46 | 2 | 3 | 1 | 10 | 16 | ||
| 56 | 3 | 5 | 1 | 4 | 13 | ||
| 66 | 8 | 2 | 1 | 11 | |||
| 76 | 1 | 2 | 3 | ||||

| 6 | 9 | 6 | 12 | 12 | 5 |  =50 =50
|
Вариант 10


| 42 | 46 | 50 | 54 | 58 | 62 | 
|
| 15 | 4 | 2 | 1 | 7 | |||
| 25 | 2 | 1 | 3 | 8 | 5 | 19 | |
| 35 | 4 | 2 | 1 | 3 | 10 | ||
| 45 | 3 | 2 | 10 | 3 | 2 | 20 | |
| 55 | 1 | 3 | 9 | 1 | 14 | ||

| 6 | 10 | 16 | 15 | 12 | 11 |  =70 =70
|
Вариант 11


| 20 | 25 | 30 | 35 | 40 | 45 | 
|
| 30 | 6 | 4 | 10 | ||||
| 40 | 4 | 1 | 5 | 7 | 17 | ||
| 50 | 3 | 4 | 5 | 6 | 18 | ||
| 60 | 5 | 3 | 10 | 2 | 20 | ||
| 70 | 2 | 3 | 3 | 5 | 13 | ||

| 12 | 12 | 12 | 19 | 12 | 11 |  =78 =78
|
Вариант 12


| 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 15 | 6 | 4 | 10 | ||||
| 25 | 6 | 8 | 14 | ||||
| 35 | 21 | 2 | 5 | 28 | |||
| 45 | 4 | 12 | 6 | 22 | |||
| 55 | 1 | 5 | 6 | ||||

| 6 | 10 | 8 | 25 | 15 | 16 |  =80 =80
|
Вариант 13


| 20 | 25 | 30 | 35 | 40 | 45 | 
|
| 10 | 4 | 8 | 4 | 16 | |||
| 20 | 2 | 4 | 2 | 8 | |||
| 30 | 10 | 8 | 18 | ||||
| 40 | 4 | 10 | 4 | 18 | |||

| 2 | 8 | 22 | 18 | 6 | 4 |  =60 =60
|
Вариант 14


| 5 | 10 | 15 | 20 | 25 | 30 | 
|
| 14 | 4 | 6 | 8 | 4 | 22 | ||
| 24 | 8 | 10 | 6 | 24 | |||
| 34 | 32 | 32 | |||||
| 44 | 4 | 12 | 6 | 22 | |||

| 4 | 14 | 46 | 20 | 12 | 4 |  =100 =100
|
Вариант 15


| 15 | 20 | 25 | 30 | 35 | 40 | 
|
| 100 | 2 | 1 | 7 | 10 | |||
| 120 | 4 | 2 | 3 | 9 | |||
| 140 | 5 | 10 | 5 | 2 | 22 | ||
| 160 | 3 | 1 | 2 | 3 | 9 | ||

| 6 | 6 | 5 | 18 | 7 | 8 |  =50 =50
|
Вариант 16


| 12 | 17 | 22 | 27 | 32 | 37 | 
|
| 105 | 4 | 3 | 7 | ||||
| 115 | 2 | 3 | 1 | 10 | 16 | ||
| 125 | 3 | 5 | 1 | 4 | 13 | ||
| 135 | 8 | 2 | 1 | 11 | |||
| 145 | 1 | 2 | 3 | ||||

| 6 | 9 | 6 | 12 | 12 | 5 |  =50 =50
|
Вариант 17


| 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 14 | 4 | 2 | 1 | 7 | |||
| 24 | 2 | 1 | 3 | 8 | 5 | 19 | |
| 34 | 4 | 2 | 1 | 3 | 10 | ||
| 44 | 3 | 2 | 10 | 3 | 2 | 20 | |
| 54 | 1 | 3 | 9 | 1 | 14 | ||

| 6 | 10 | 16 | 15 | 12 | 11 |  =70 =70
|
Вариант 18


| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 5 | 10 | 3 | 5 | 1 | 4 | 23 | ||
| 15 | 4 | 10 | 2 | 8 | 24 | |||
| 25 | 3 | 4 | 6 | 6 | 19 | |||
| 35 | 4 | 7 | 1 | 5 | 17 | |||
| 45 | 2 | 5 | 10 | 17 | ||||

| 15 | 13 | 13 | 15 | 19 | 10 | 15 |  =100 =100
|
Вариант 19

 j j
| 24 | 28 | 32 | 36 | 40 | 44 | 48 | 
|
| 10 | 6 | 4 | 2 | 5 | 17 | |||
| 20 | 4 | 5 | 7 | 1 | 17 | |||
| 30 | 4 | 3 | 5 | 6 | 18 | |||
| 40 | 5 | 3 | 10 | 2 | 20 | |||
| 50 | 4 | 10 | 4 | 2 | 8 | 28 | ||

| 9 | 13 | 12 | 19 | 21 | 7 | 19 |  =100 =100
|
Вариант 20


| 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 36 | 4 | 3 | 7 | ||||
| 46 | 2 | 3 | 1 | 10 | 16 | ||
| 56 | 3 | 5 | 1 | 4 | 13 | ||
| 66 | 8 | 2 | 1 | 11 | |||
| 76 | 1 | 2 | 3 | ||||

| 6 | 9 | 6 | 12 | 12 | 5 |  =50 =50
|
Вариант 21


| 42 | 46 | 50 | 54 | 58 | 62 | 
|
| 15 | 4 | 2 | 1 | 7 | |||
| 25 | 2 | 1 | 3 | 8 | 5 | 19 | |
| 35 | 4 | 2 | 1 | 3 | 10 | ||
| 45 | 3 | 2 | 10 | 3 | 2 | 20 | |
| 55 | 1 | 3 | 9 | 1 | 14 | ||

| 6 | 10 | 16 | 15 | 12 | 11 |  =70 =70
|
Вариант 22


| 20 | 25 | 30 | 35 | 40 | 45 | 
|
| 30 | 6 | 4 | 10 | ||||
| 40 | 4 | 1 | 5 | 7 | 17 | ||
| 50 | 3 | 4 | 5 | 6 | 18 | ||
| 60 | 5 | 3 | 10 | 2 | 20 | ||
| 70 | 2 | 3 | 3 | 5 | 13 | ||

| 12 | 12 | 12 | 19 | 12 | 11 |  =78 =78
|
Вариант 23


| 12 | 17 | 22 | 27 | 32 | 37 | 
|
| 105 | 4 | 3 | 7 | ||||
| 115 | 2 | 3 | 1 | 10 | 16 | ||
| 125 | 3 | 5 | 1 | 4 | 13 | ||
| 135 | 8 | 2 | 1 | 11 | |||
| 145 | 1 | 2 | 3 | ||||

| 6 | 9 | 6 | 12 | 12 | 5 |  =50 =50
|
Вариант 24


| 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 14 | 4 | 2 | 1 | 7 | |||
| 24 | 2 | 1 | 3 | 8 | 5 | 19 | |
| 34 | 4 | 2 | 1 | 3 | 10 | ||
| 44 | 3 | 2 | 10 | 3 | 2 | 20 | |
| 54 | 1 | 3 | 9 | 1 | 14 | ||

| 6 | 10 | 16 | 15 | 12 | 11 |  =70 =70
|
Вариант 25


| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 
|
| 5 | 10 | 3 | 5 | 1 | 4 | 23 | ||
| 15 | 4 | 10 | 2 | 8 | 24 | |||
| 25 | 3 | 4 | 6 | 6 | 19 | |||
| 35 | 4 | 7 | 1 | 5 | 17 | |||
| 45 | 2 | 5 | 10 | 17 | ||||

| 15 | 13 | 13 | 15 | 19 | 10 | 15 |  =100 =100
|
ПРОВЕРКА ГИПОТЕЗЫ О ЗАКОНЕ РАСПРЕДЕЛЕНИИ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ.
КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА
Практическая часть
Пример 9.1. При обследовании 2000 тепличных хозяйств было отобрано 110 теплиц. Распределение их по объему совокупных ежегодных продаж (ден. ед.) приведено в таблице:
| Размер объема совокупных ежегодных продаж (ден.ед.) | менее 500 | 500 - 1000 | 1000 - 1500 | 1500 - 2000 | 2000 - 2500 |
| Число теплиц | 8 | 25 | 47 | 18 | 12 |
Используя критерий  Пирсона, при уровне значимости
Пирсона, при уровне значимости  = 0,05 проверить гипотезу о том, что случайная величина Х – размер объема совокупных ежегодных продаж распределена по нормальному закону.
= 0,05 проверить гипотезу о том, что случайная величина Х – размер объема совокупных ежегодных продаж распределена по нормальному закону.
Решение:
По условию N = 2000 (объем генеральной совокупности), n = 110 (объем выборки). Найдем середины интервалов
| Варианты | 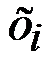
| 250 | 750 | 1250 | 1750 | 2250 |
| Частоты | 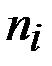
| 8 | 25 | 47 | 18 | 12 |
Найдем числовые характеристики выборки
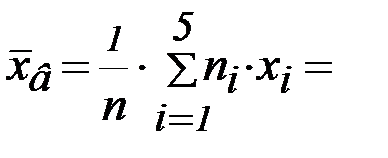
= 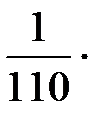 (8·250 + 25·750 + 47·1250 + 18·1750 + 12·2250) = 1254,5;
(8·250 + 25·750 + 47·1250 + 18·1750 + 12·2250) = 1254,5;
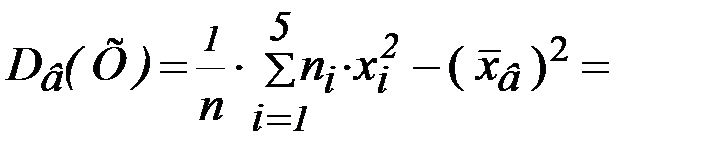
= 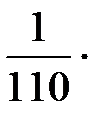 (8·
(8· 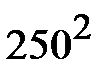 +25·
+25· 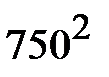 +47·
+47· 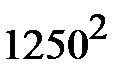 +18·
+18· 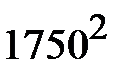 +12·
+12· 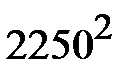 ) –
) – 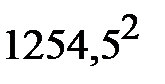 =
=
= 279524,679;
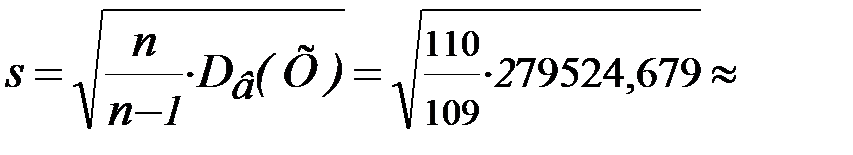 531,121.
531,121.
Используя критерий согласия Пирсона, при уровне значимости  = 0,05 проверим гипотезу
= 0,05 проверим гипотезу 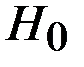 : о нормальном распределении случайной величины Х с параметрами а =
: о нормальном распределении случайной величины Х с параметрами а = 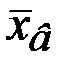 = 1254,5 и
= 1254,5 и 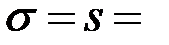 531,121 при альтернативной гипотезе
531,121 при альтернативной гипотезе 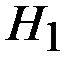 : «Случайная величина Х не распределена по нормальному закону».
: «Случайная величина Х не распределена по нормальному закону».
Вычислим вероятности 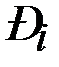 попадания случайной величины Х в заданные интервалы с помощью функции Лапласа (таблица прил. 1):
попадания случайной величины Х в заданные интервалы с помощью функции Лапласа (таблица прил. 1):
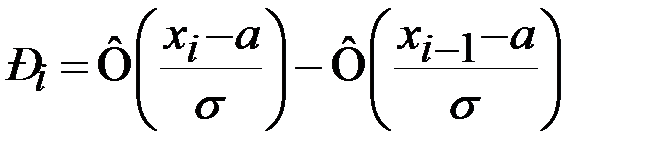 .
.
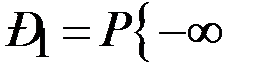 <
< 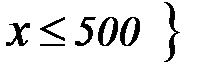 = Ф(– 1,42) – Ф(
= Ф(– 1,42) – Ф(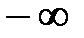 ) = – 0,4222 + 0,5 = 0,0778;
) = – 0,4222 + 0,5 = 0,0778;
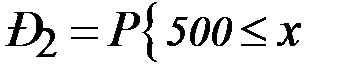 <
< 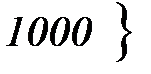 = Ф(– 0,48) – Ф(– 1,42) = – 0,1844 + 0,4222 = 0,2378;
= Ф(– 0,48) – Ф(– 1,42) = – 0,1844 + 0,4222 = 0,2378;
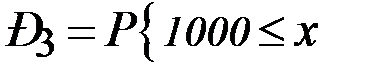 <
< 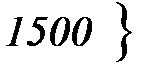 = Ф(0,46) – Ф(– 0,48) = 0,1772 + 0,1844= 0,3616;
= Ф(0,46) – Ф(– 0,48) = 0,1772 + 0,1844= 0,3616;
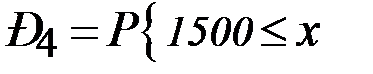 <
< 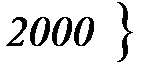 = Ф(1,40) – Ф(0,46) = 0,4192 – 0,1772= 0,2420;
= Ф(1,40) – Ф(0,46) = 0,4192 – 0,1772= 0,2420;
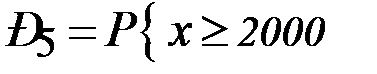
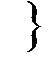 = Ф(
= Ф(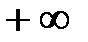 ) – Ф(1,40) = 0,5 – 0,4192= 0,0808.
) – Ф(1,40) = 0,5 – 0,4192= 0,0808.
Для проведения расчетов заполним таблицу
Т а б л и ц а 9.1
интервал
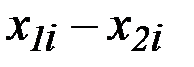
| частота
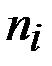
| теоретическая частота
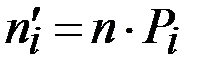
| 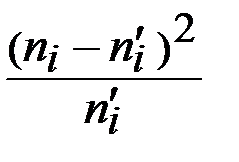
| 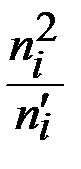
|
| менее 500 | 8 | 8,558 | 0,0364 | 7,4784 |
| 500 - 1000 | 25 | 26,158 | 0,0513 | 23,8933 |
| 1000 - 1500 | 47 | 39,776 | 1,3120 | 55,5360 |
| 1500 - 2000 | 18 | 26,62 | 2,7913 | 12,1713 |
| 2000 - 2500 | 12 | 8,888 | 1,0896 | 16,2016 |
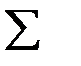
| 110 | 110 | 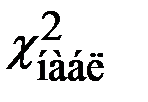 = 5,2806 = 5,2806
| 115,2806 |
Контроль: 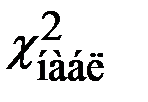 = 5,2806;
= 5,2806; 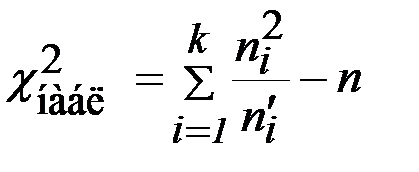 = 115,2806 – 110 = 5,2806.
= 115,2806 – 110 = 5,2806.
Вычисления произведены правильно.
По таблице прил. 3 по заданному уровню значимости  = 0,05 и числу степеней свободы
= 0,05 и числу степеней свободы 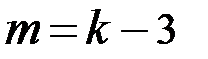 = 5 – 3 = 2 найдем критическое значение
= 5 – 3 = 2 найдем критическое значение
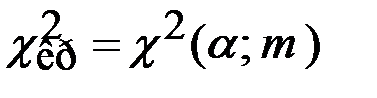 =
= 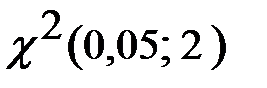 = 6,0.
= 6,0.
Так как 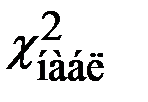 = 5,2806 <
= 5,2806 < 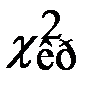 = 6,0, то нулевая гипотеза о нормальном распределении принимается как не противоречащая опытным данным.
= 6,0, то нулевая гипотеза о нормальном распределении принимается как не противоречащая опытным данным.
 2020-10-09
2020-10-09 275
275








