Практическая часть
Пример 5.1. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить ряд распределения числа стандартных деталей среди отобранных. Найти числовые характеристики. Какова вероятность того, что среди отобранных деталей хотя бы одно будет стандартным?
Решение. Случайная величина X – число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: x1=0, x2=1, x3=2. Найдем вероятности возможных значений X по формуле
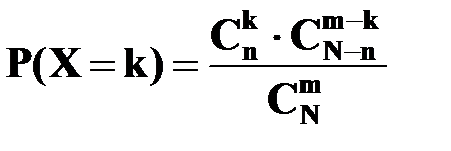 ,
,
где N – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных.
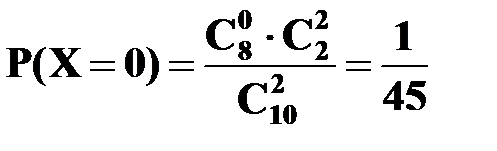 ,
,
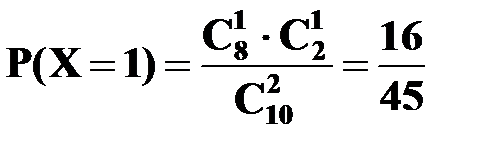 ,
,
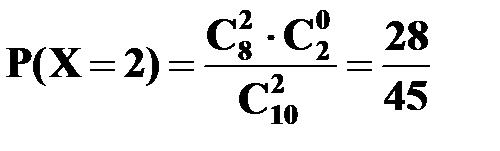 .
.
Составим искомый ряд распределения:
| X | 0 | 1 | 2 |
P 
| 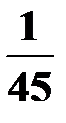
| 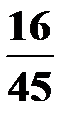
| 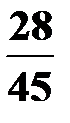
|
Контроль: 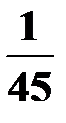 +
+ 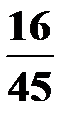 +
+ 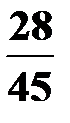 =1.
=1.
Найдем числовые характеристики случайной величины X.
M(X) = 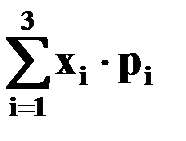 =
= 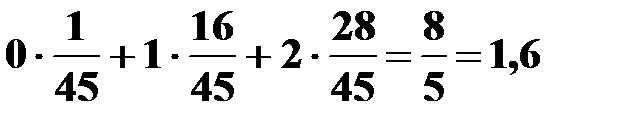 ;
;
D(X) = 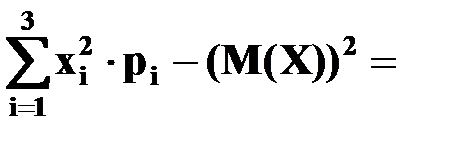
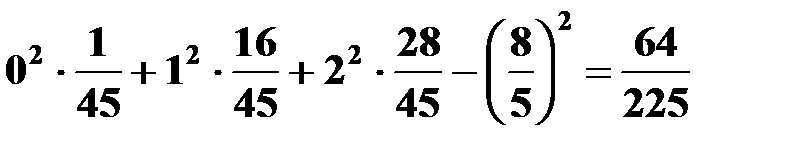 ;
;
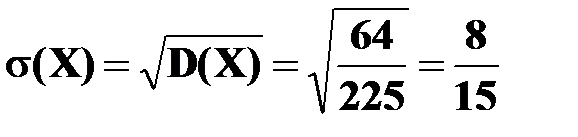 .
.
Пусть событие В -среди отобранных деталей хотя бы одно будет стандартным. Рассмотрим событие 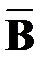 , противоположное событию В:
, противоположное событию В:
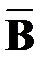 - среди отобранных деталей нет стандартных, P(
- среди отобранных деталей нет стандартных, P( 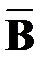 )=P(X=0)=
)=P(X=0)= 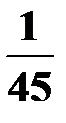 . Тогда
. Тогда
P (B) =1 – P ( 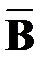 ) =1 –
) =1 – 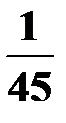 =
= 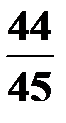 .
.
Пример 5.2. В рейс выделено 3 автобуса. Вероятность того, что во время рейса автобус будет работать без поломок, равна 0,9. Составить ряд распределения дискретной случайной величины Х – числа автобусов, работающих без поломок в течение рейса. Найти числовые характеристики. Чему равна вероятность того, что более одного автобуса будут работать безотказно?
Решение. Дискретная случайная величина X (число автобусов, работающих без поломок в течение рейса) имеет следующие возможные значения: x1=0, x2=1, x3=2, x4=3.
Автобусы работают независимо один от другого, вероятности безотказной работы каждого автобуса равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n =3, p=0,9, q=1 – p=0,1, получим:
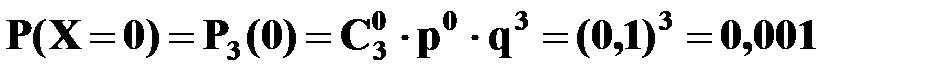 ,
,
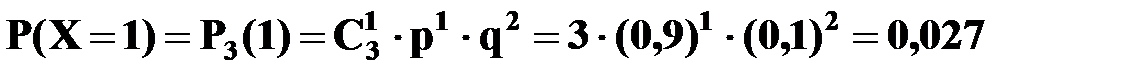 ,
,
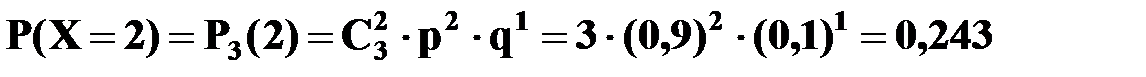 ,
,
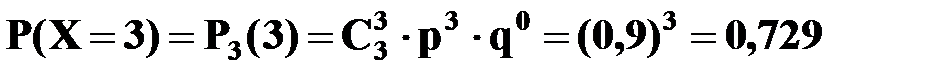 .
.
Контроль: 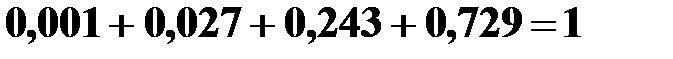 .
.
Напишем искомый ряд распределения:
| X | 0 | 1 | 2 | 3 |
| P | 0,001 | 0,027 | 0,243 | 0,729 |
Найдем числовые характеристики случайной величины X.
M(X) = 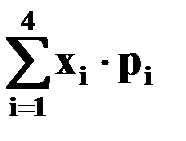 =
= 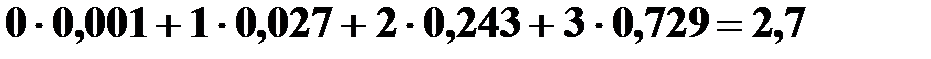 ;
;
D(X) = 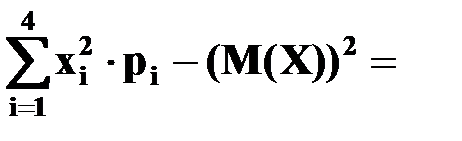
= 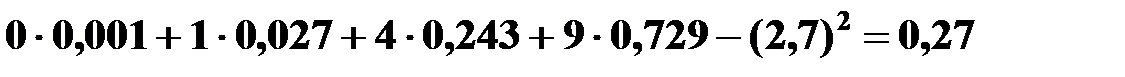 ;
;
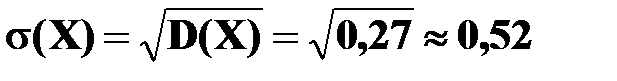 .
.
Пусть событие В -более одного автобуса будут работать безотказно, т. е. или два, или три автобуса.
P (B) =P(X=2) +P(X=3) =0,243+0,729=0,972.
Пример 5.3. Независимые случайные дискретные величины X, Y заданы законами распределения.
| X | -6 | -3 | 1 | 2 |
| P | 0,4 | 0,3 | р | 0,1 |
| Y | -2 | 8 |
| P | 0,2 | 0,8 |
Найти:
1) р;
2) функцию распределения случайной величины X и построить ее график;
3) математическое ожидание и дисперсию случайной величины Z=2X-4Y.
Решение.
1) В результате опыта случайная величина X примет только одно из возможных значений 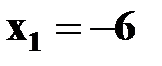 ,
, 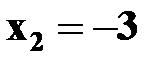 ,
, 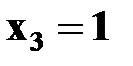 ,
, 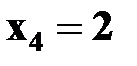 , т. е. произойдет только одно из полной группы событий. Поскольку сумма вероятностей полной группы попарно несовместных событий равна 1, то
, т. е. произойдет только одно из полной группы событий. Поскольку сумма вероятностей полной группы попарно несовместных событий равна 1, то
0,4+0,3+р+0,1=1.
Следовательно, р=1-0,4-0,3-0,1=0,2.
Таким образом, ряд распределения случайной величины Х имеет вид
| X | -6 | -3 | 1 | 2 |
| P | 0,4 | 0,3 | 0,2 | 0,1 |
2) Найдем функцию распределения F(X).
Если 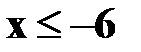 , то F(x)=0.
, то F(x)=0.
Действительно, значений, меньших числа 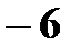 , величина X не принимает. Следовательно, при
, величина X не принимает. Следовательно, при 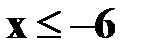 функция F(x)=P(X<x)=0.
функция F(x)=P(X<x)=0.
Если 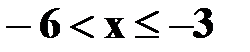 , то F(x)=0,4.
, то F(x)=0,4.
Действительно, X может принимать значение 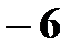 с вероятностью 0,4.
с вероятностью 0,4.
Если 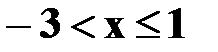 , то F(x)=0,7.
, то F(x)=0,7.
Действительно, X может принимать значение 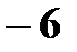 с вероятностью 0,4 и значение
с вероятностью 0,4 и значение 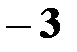 с вероятностью 0,3; следовательно, одно из этих значений, безразлично какое, X может принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0,4+0,3=0,7.
с вероятностью 0,3; следовательно, одно из этих значений, безразлично какое, X может принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0,4+0,3=0,7.
Если 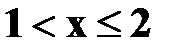 , то F(x)=0,9.
, то F(x)=0,9.
Действительно, X может принимать значение 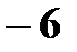 с вероятностью 0,4, значение
с вероятностью 0,4, значение 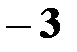 с вероятностью 0,3, значение 1 с вероятностью 0,2; следовательно, одно из этих значений, безразлично какое, X может принять с вероятностью 0,4+0,3+0,2=0,9.
с вероятностью 0,3, значение 1 с вероятностью 0,2; следовательно, одно из этих значений, безразлично какое, X может принять с вероятностью 0,4+0,3+0,2=0,9.
Если 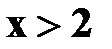 , то F(x)=1.
, то F(x)=1.
Действительно, событие 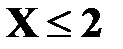 достоверно и вероятность его равна единице.
достоверно и вероятность его равна единице.
Итак, искомая функция распределения имеет вид

График этой функции приведен на рисунке.
F(x)
1
0,9
0,7
0,4
-6 -3 0 1 2 x
3) Найдем математическое ожидание случайных величин X, Y.
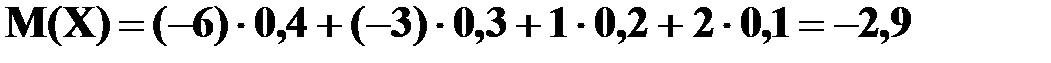 ;
;
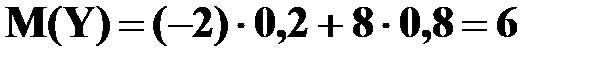 .
.
Используя свойства математического ожидания, получим
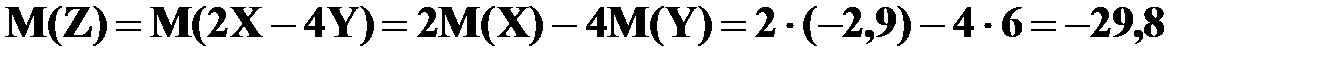 .
.
Найдем дисперсии случайных величин X, Y.
D(X)= 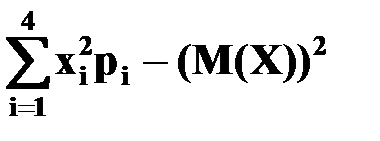 =
=
= 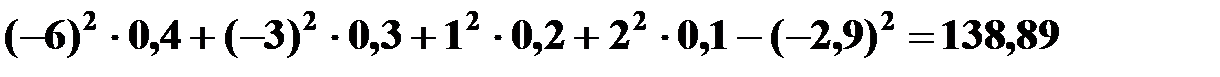 ;
;
D(Y) = 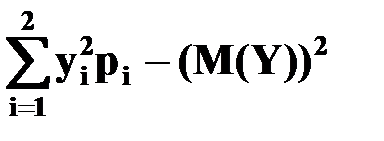 =
= 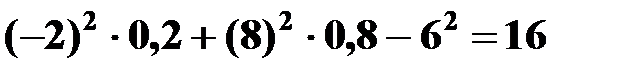 .
.
Так как величины X и Y независимы, то независимы также и величины 2X и 4Y. Используя свойства дисперсии, получим
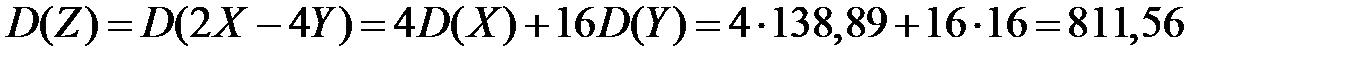 .
.
 2020-10-09
2020-10-09 440
440








